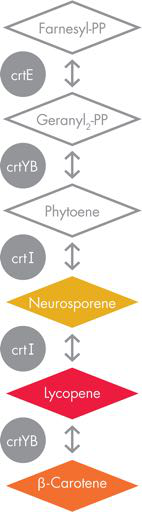
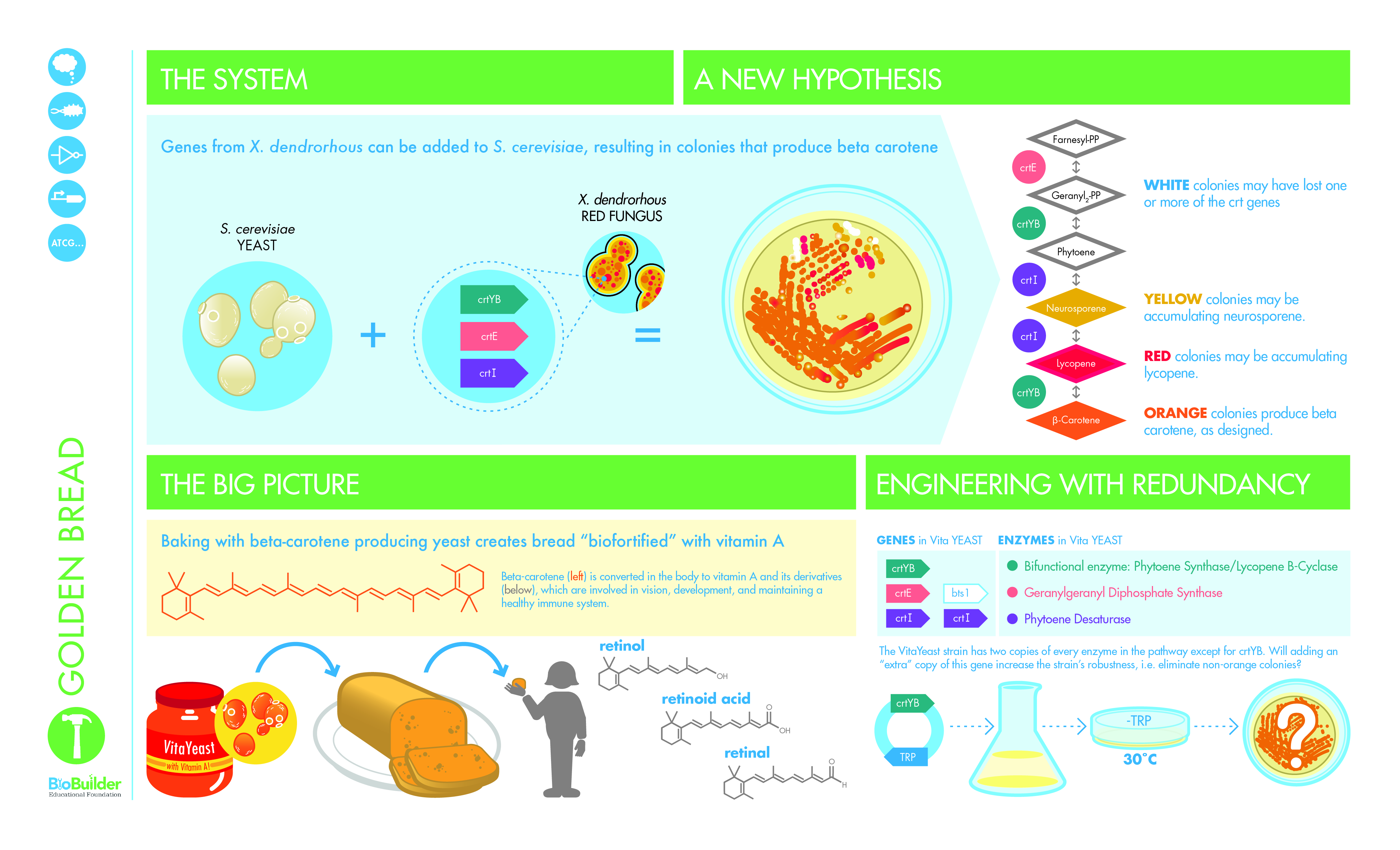
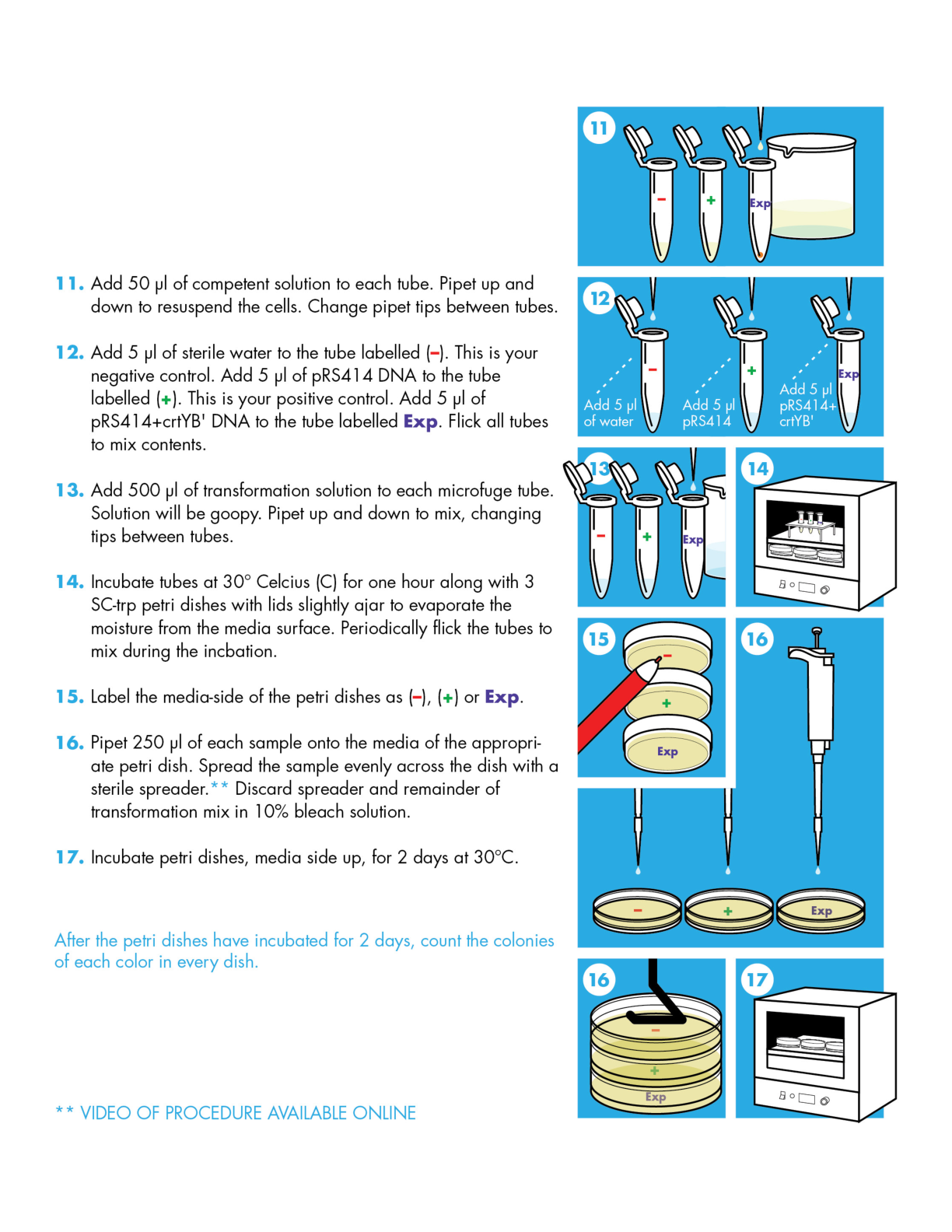
A Revelation of the Apocalypse

The Apocalypse of St. John, illustrated with an analysis and scholia, in which the meaning is explained by Scripture and the predicted events are shown by histories. A general overview is prefixed hereunto; and at the end of the seventeenth chapter is inserted a refutation of Robert Bellarmine concerning Antichrist, in his third book on the Bishop of Rome. By Thomas Brightman.

CHAPTER 2. (BOOK 2)
1 To the Angel of the Church of Ephesus write, these things says he, that holds those seven stars in his right hand, which walk in the midst of the seven candlesticks;
2 I know your works and your labor, and your patience, and that you cannot suffer the wicked: and have tried them, which say that they are apostles and are not, and have found them liars.
3 And you were burdened, and do endure, and for my name have labored and were not weary.
4 But I have something against you, that you have left your first love.
5 Be mindful therefore from whence you are fallen, and do the first works; or else I will come against you shortly, and remove your candlestick from its place, unless you do repent.
6 But this you have, that you hate the works of the Nicolaitans, which I also hate.
7 Let him that has an ear hear what the spirit says to the Churches, to him that overcomes I will give to eat of that tree of life, which is in the midst of the Paradise of God.
8 To the Angel of the Church of Smyrna write, these things says he that is the first and last, who was dead, and is alive.
9 I know your works and your affliction, and poverty (but you are rich) and the blasphemy of those who say they are Jews and are not, but the synagogue of Satan.
10 Fear none of those things which you will suffer: Behold it shall come to pass, that Satan shall cast some of you into prison, that you may be tried; and you shall have affliction ten days: Be faithful unto death, and I will give you the crown of life.
11 Let him that has an ear, hear what the spirit says to the Churches. He that shall overcome, shall not be hurt by the second death.
12 And to the Angel of the Church of Pergamus write, these things says he, that has that sharp two‑edged sword.
13 I know your works, and where you dwell, to wit, where Satan’s throne is, and that you keep my name, and have not denied my faith, yea even in those days in which Antipas that my faithful martyr was slain among you, where Satan dwells:
14 But I have a few things against you, that you have there those who hold the doctrine of Balaam, who taught Balak to lay a stumbling block before the children of Israel, that they should eat of those things, which were offered to idols, and that they should commit fornication,
15 So also have you them, which hold the doctrine of the Nicolaitans, which I hate.
16 Repent: or else I will come against you quickly and fight with them, with that sword of my mouth.
17 Let him that has an ear, hear what the spirit says to the Churches: I will give to him that overcomes, to eat of the hidden manna, and I will give him a white stone, and a new name written in the stone, which no man knows, but he that receives it.
18 And to the Angel of the Church of Thyatira, write, these things says the Son of God, which has eyes as a flame of fire, and whose feet are like fine brass.
19 I know your works, and love, and service, and faith, and patience, and your works, and your last are more than the first.
20 But I have a few things against you, that you suffer the woman Jezebel, which says she is a prophetess, to teach and deceive my servants, that they should commit fornication and eat of things which are offered to idols.
21 And I gave her time to repent of her fornication: but she has not repented.
22 Behold I will cast her into a bed and them that commit adultery with her into very great affliction, unless they repent of their works.
23 And I will kill her children with death, and all the Churches shall know that I am the searcher of the reins and of hearts, and I will give to every one of you according to your works.
24 And to you I say, and the rest of the Thyatirians, whosoever holds not this doctrine and who have not known the depths of Satan, as they say: I will lay no other burden upon you;
25 Yet that which you have, keep till I shall come:
26 For if any shall overcome, and observe my works unto the end, I will give him power over nations.
27 And he shall rule them with a rod of iron, and they shall be broken in pieces as earthen vessels, as I also have received of my father.
28 And I will give him the morning star.
29 Let him that has an ear, hear what the spirit says to the Churches.

The Resolution. Until now, in common, that which pertains to all the seven churches: that which is proper to each one follows, an epistle being inscribed to each one separately. In each of them there is an inscription, narration, and conclusion. The first three concern churches falling into a worse state: Ephesus, Smyrna, and Pergamum. The other four return to the same, and as the next three are opposed to the first three and are answerable to each other: the Thiatiris to the Ephesians, the Sardis to the Smyrna, the Philippi to the Pergamon. Only Laodicea has no equal to which it may be compared.

Regarding the Ephesian, which holds the first place, the inscription is addressed to the angel by name, describing him as the one who gave the epistle: he holds the seven stars in his right hand and walks amid the candlesticks, verse 1.
The narration, partly respectful praise, commends their labor, patience, and discipline, verse 2.
Then their unwearied desire, verse 3.
Partly reproach, which shows their sin, their first love lost, verse 4.
And the remedy, which he first proposes, teaches what it consists of, in care of their first works; afterward he urges them to use it, partly by denouncing the removal of the candlestick unless it is done in time, verse 5.
Partly by a rehearsal of the cause for which they had been spared hitherto, verse 6.
The conclusion is both epiphonetic, requiring attention, and also rewarding: where the reward is the power to eat from the tree of life, verse 7.
The other analyses shall follow in each of their places.

Scholions.
1 TO the Angel: Every one of the Epistles is inscribed to the pastors, not so that they should keep them private to themselves, but so that they should communicate them with the rest of the church, as has been said before in ch. 1.11. Send them to the seven churches in Asia—Ephesus, Smyrna, etc.—and at the end of each let the reader hear what the Spirit says, not only to the angel but to the churches. They are sent to him by name, partly because he is the dispenser of doctrine, exhortation, reproof, etc., as the use of the church requires. Partly because the safety of the whole congregation rests chiefly upon the integrity of the pastors. Neither are they sent to any one angel, but to the whole, that I may so say, the college of pastors, who are all encompassed by this common term. For there was not one angel of Ephesus, but many, and no prince among them, as is evident from Paul, who sent to Miletus for the elders or bishops of Ephesus (Acts 20:17–28). He would have spared the multitude if anyone had been over them in authority, or at least, wise among his admonitions, he would have spoken one word of obedience to the chief bishop. But this preeminence and principality had not yet been established; it began first after the apostles were removed from human affairs, except that Diotrephes gave some indication thereof.

Therefore, under the name of one Angel, he writes to the whole order of Pastors, for whose praise or disparagement the chief purpose of every epistle is intended. For this is, for the most part, the condition of particular congregations, as their faithfulness and diligence shall be. From this, it follows that at the end the admonition is given to the whole congregation, fitted for the administration by the teachers.

Neither is it to be thought that these epistles were sent separately, and asunder one from another, but that all were written together in a common epistle, such as we have said this whole prophecy is, and that each church obtained from there that which belongs to them separately. And these things are common to all the seven angels, to be applied to every one apart.

¶ To the Church of Ephesus: Of the city Ephesus we have spoken briefly in the eleventh verse of the first chapter: to which are to be added the reason of the order, the force of the name, and the antitype of it, that the counsel of the spirit may be better understood. There may be a double reason for the order: one is that this city settles before our eyes as the Church of the Gentiles, like the Prodigal son who spent his patrimony in a far country (Luke 15:11). And when he returns, we see Christ as an image of the conversion and calling of the Gentiles.

For this city, besides the horrible idolatry of which she was a leader of other cities, it was also subject to great riot, casting out of the city a certain man called Hermodorus, not for any other crime than that he was a thrifty man. Moreover, it is added: Let no one of us excel, but if there be any such, let him be in another place among other men. Tusc. quest. book 5. leaf 125. a voice indeed of beasts, and even in the sentence of Ethnics, worthy of a halter.

For thus says Strabo: All the Ephesians are to be punished by death. Behold, therefore, the prodigal son, coming again to his father, running to meet him, falling to his neck, and kissing him. How is the grace of God to be praised, who has converted us Gentiles, being a gulf of wickedness, the disposition of all which we see in this city, into a most glorious palace of salvation.

We were once princes of naughtiness; now we have become the head of holiness, as among the seven churches: no less excelling in godliness than we did in all wickedness of late. For the Father has commanded the best robe to be brought forth and has killed the fattened calf for our sake.

Another reason for the order is that this city was foremost in embracing faith among all that country, from which it spread to neighboring places. For Paul, coming to Ephesus, was daily disputed in the school of one Tyrannus, and over the space of two years, so that all who dwelt in Asia—both Jews and Gentiles—heard the word of the Lord Jesus (Acts 19:9–10). Therefore it is well made in the same place, the beginning of cities, from which faith began.

Now the force of the name is to be declared. For it shall be clear to everyone that the Holy Ghost has chosen those churches, which even by their very names, as it were by certain marks written on the forehead, should manifest their whole condition. We let pass that Amazon, from whom they report that it took the name, that which follows beneath verse 4, that thou hast left thy first love, teaches sufficiently what the Spirit regarded in this city: namely that Ephesus was, as it were, an omission, whereupon we call her languishing, whose godliness wavered cold in such a sort that at length it is utterly extinguished. How is it to be feared that in this thing also it carries a type of the Gentiles!

Regarding the antitype, we observe that these seven cities embody the universal condition of the churches of the Gentiles. As is clearly stated in the first chapter, each city is not only to be considered on its own, but also the neighboring church that may be directly related to it. What kind of antitypes are these? Were these seven churches meant to be patterns for all churches of that time, or for churches of different times? If we say the former, then in all ages the church spread throughout the world, it agreed with those seven; that is, one should be Ephesus, one Smyrna, one Pergamum, and so on. The same form should have existed in the first times and should exist today, as the teaching of all times dictates. Therefore it is necessary to treat each of them as separate types, in the order in which they are listed. The antitypes are those churches that, whether divided by time or by place, agree with each other in order. The convenience of the matter will become clear within the limits of these conclusions. According to this rule, we make the first Christian church the antitype of the city of Ephesus, which, drawing from the preaching of the apostles, continued even until Constantine the Great, as will be made manifest in what follows. This is the chief of all the following churches, as Ephesus is the first of the seven cities.

¶ These things say he that holds the seven stars: A description of him that sent the Epistles, which is diverse in every part, yet drawn from the former vision, diverse members of it being applied according to the diverse conditions of things. Which teaches abundantly, both the whole former figure to have shadowed out only the administration of things, and also to be proper in a manner and peculiar to the seven Churches. The seven stars in his right hand declare that the power of Christ is notable in defending the Ministers of this Church. He is even as mighty a keeper and faithful maintainer of all his faithful servants, in whatever place of the earth, or whatever timesoever they have been or shall be; yet in some certain places and times, he manifests himself more clearly to the world as an avenger, than everywhere else, as appears both in this city and antitype. As touching the city, Paul, who planted the faith there first, how many adversaries did he find there? I will abide, says he, at Ephesus till Pentecost, for a great door and effectual is opened to me, and the adversaries many: 1 Cor. 16:9. Yet we read not that any calamity came unto him. He was beaten elsewhere and stoned and left for dead: but here Demetrius stirring up the workmen against him, he that holds the stars in his right hand, not only kept Paul free from all evil, but also Caius and Aristarchus and Alexander, pacifying the tumult by the prudence of the town clerk; Acts 19. The same hand shielded Tychicus and Timotheus, the Angels thereafter of the same Church: Ephes. 6:21. 1 Tim. 1:3. And no less the Elders, the ordinary Bishops of the Church, whom Paul called to Miletus to give them his last farewell. At length John came to the same place, and there abode many years, establishing all the neighboring Churches. Neither did the rage of the tyrant proceed to his death: but at length returning from banishment, he died quietly in this city. The power of the mighty and star‑bearing hand gave such safety to his servants. The same power also shone forth in preserving the Pastors through the whole time of the first Church. A huge number indeed of the faithful were slain daily, but this is marvelous, that in the opinion of men it being necessary that the name of Christ should be extinguished utterly, much more the Pastors, against whom the Tyrants raged most of all, there was a daily great increase, that it was spoken then commonly and truly: That the blood of the Martyrs is the seed of the Church. But Christ walks among the candlesticks, as often as he gives a manifest proof of himself being present and regarding diligently all things which pertain to the salvation of the faithful. In what city did he give a show of more plentiful grace and favour, than in Ephesus, to whom for teachers he gave Paul, Apollos, Tychicus, Timotheus, John the Apostle, besides many other Apostolic men? And where or when was Christ more manifestly conversant in the earth since his ascension into Heaven, than in those first times, until about Constantine? He did enrich so abundantly the Church with all gifts, he pricked forward their sluggishness, corrected their negligence, rewarded their virtue, so as he might seem by himself to compass every one, and view their labour with his own eyes. In one and the same manner he is always among the candlesticks, neither does he sit idly, but walks about continually, and comes to visit everything, so that he has no need of a vicar: yet because by outward arguments, this is not often manifested to the world, therefore that which is properly and singularly belonging as it were to one city and time, is alleged.

¶ I know thy works: A narration, and first of praise. And it is common to all the Epistles, in the beginning of the narration, to profess that he knows certainly and tries every angel’s works. Therefore neither shall reward be wanting at any time to virtue, nor just punishment to naughtiness. And as even now I have put in mind of a Vicar, how wickedly serviceable are they, who arrogate to themselves, as an absolute lord, the power over their fellow servants, seeing he thoroughly knows all things, and is not in vain conversant among the candlesticks? The praise of the Ephesians Angel respects either his office, in this verse, or his virtue against outward evils, ver. 3. His office consists, either in administering the word and those things which are wont to accompany it usually, the Sacraments and prayers, or in exercising of discipline. As he says, I know thy labor and thy patience: For the pains which are bestowed in preaching the word, because it is laborious, and full of troubles and grief, is wont to be called labor in the scriptures, as, we pray you brethren that ye as know them that labor among you; &c. 1 Thessalonians 5:12. And they are worthy of double honor: especially they that labor in the word and doctrine: 1 Timothy 5:17. But patience as a necessary companion must be added to the labor of teaching: which the Spirit shows, saying, and your patience. As also Paul, the servant of God must not fight, but must be gentle toward all men, apt to teach, suffering from evil men: teaching them with meekness that is contrary-minded: 2 Timothy 2:23-24. Therefore this church was famous in the faithfulness and diligence of teaching. Behold the example of Paul, who by the span of three years, day and night, ceased not to admonish everyone with tears: Acts 20:31. Do thou also consult from those godly bishops, who loved Paul so greatly, whom also he again loved no less: Acts 20:37-38. Afterwards mind John and the rest. But a matter that is clear need not many words.

As touching her Antitype, the matter is even evident; they never more faithfully gave themselves to teaching. That monster was not yet born, that any should be a pastor, that does not feed at all; or that one should sit in the chair of the teacher, who, being dumb, should be sleepy and distracted with other businesses. There was then no bishop who had the office of teaching and who did not teach most diligently. Even in Rome, where it was fitting that the mystery of iniquity should spring up early, they had not yet ceased from this office. The pastor, at least on every Lord’s Day, plainly and clearly expounded those things that were read from the books of the apostles and prophets. He also admonished and exhorted them to follow those things, which, being holy and good, they had heard rehearsed: Justin, Apolog. 2. The same thing is testified by Clemens, Origen, Tertullian, and Cyprian. But the matter is so clear and manifest that it should be done contrary to this at this day.

¶ And that you cannot bear the wicked: Such was the care of teaching, the manner of their discipline was no less pure and sound: Which first is universally set down, of what sort it was toward all the wicked: afterward specially, what it was toward the clergy, that I may so speak, in the next words, and has tried them which say they are apostles, etc. The general discipline did not tolerate men in any sort living wickedly, and with the offense of others, but according to the manner of their fault, rebuked either privately or before many, if private admonition was unprofitable; then finally it debarred them from holy things if they would not obey those who counseled them well. Regarding Ephesus, it cannot be uncertain, but that this holy rule held there, since Paul taught there for three years, who gave a command to Timothy regarding this matter so diligently and exactly. The observation thereof was famous in the primitive church, as even Pliny testifies in an epistle to Trajan: The Christians are wont, he says, to rise early in the morning to praise Christ as God, for the preservation of their religion, to prohibit murders, adulteries, avarice, cozenage, and the like unto those: Eusebius, book 3, chap. 33, of the Ecclesiastical History from Tertullian. They not only prohibited in word by teaching but also restrained them by holy discipline. They rightly determined that religion could not be preserved otherwise, unless vices be cut off by this spiritual sword. Justin testifies that no man was admitted to the sacrament of the supper except he whose life should answer and accord with his profession, Apoll. 2. But more plainly Tertullian writes thus: There are also exhortations, corrections, and divine censure: it is shown with great gravity that if anyone has offended, he may be sent away from communicating in prayer, both of the assembly and all holy society, where all most approved elders have authority, having obtained that honour not by money but by good report: Apologetics, ch. 39. Origen in his 35th treatise on Matthew. In the churches of Christ, he says, such a custom has held that those who are manifest in great sins, of whom they are convicted, should be cast out from common prayer lest a little leaven of those who pray not from their heart corrupt the whole sprinkling and consent of truth. So in Homily 7 on Joshua: He who, being admonished a third time, refuses to repent, is commanded to be cut off from the body of the church by its rulers. He also shows that priests, sparing one, and neglecting their priestly severity, do work the ruin of the whole church. The epistles of Cyprian are clear witnesses of how holy and religiously he kept it in his church; they also prove how purely the discipline abided hitherto in Rome, as is clear from the epistles of Cyprian to the clergy of Rome, and to Cornelius, and again from them to Cyprian. It is therefore an excellent testament of that time, which, combined with purity of doctrine and sanctity of manners, demonstrates the most wholesome discipline.

¶ And have tried them who say they are apostles. The other part of discipline is toward ecclesiastical men, who were reproved not only for sins in life, but also punished for their ungodliness if they introduced any new ideas and deviated from the truth, which, after proper examination, were found not to agree with the rules of the sanctuary. And great was the courage of the angel in this matter; he was not deterred by great names, but brought them back to a thorough examination, where they boasted they were apostles. It is clear that there were men in Ephesus, as is evident from the instruction given to Timothy: “You should remain in Ephesus so that you may warn some, that they teach no other doctrine, nor listen to endless fables and genealogies that raise questions rather than godly edification, which is by faith.” (1 Timothy 1:3). And Paul also warned the bishops of Ephesus to take care of themselves and the whole flock: “I know that after my departure, fierce wolves will come among you, and some of your own will arise, speaking perverse things, so that they may lead disciples after them.” (Acts 20:29‑30). But the diligence of the pastors removed the deceivers from the hypocrites and did not allow their craft to spread to the destruction of the flock, so the church remained uncorrupted even up to the time of John, who ruled for many years: who eventually, for a time, withdrew, and the care slackened somewhat, as we shall show later. Likewise, in the early church there was such a group of heretics as rare as in all other times. There arose Simonians, Menanderists, Ebionites, Cerinthians, Pseudoapostles, Gnostics, Sabellians, Samosatenians, Manichees, etc. Some of these the apostles themselves pierced with the dart of truth. Paul taught Titus to shun a heretical man after one or two admonitions: Titus 3:10. But after they turned to Christ, many other bright lights rose up, diligently dispelling all heretical darkness. Among them were Agrippa Castor, as Eusebius reports, Justin Martyr, Irenaeus, Tertullian, Cyprian, etc., all of whom fought eagerly for truth against counterfeit apostles. Therefore, as both the city and that former age were perilous due to the impudence of those who, with false titles, claimed to be apostles, they were not less happy thanks to the faithfulness and diligence of such defenders, who were not deceived by a vain show, but brought the matter to the touchstone and showed the whole church that they were most filthy fellows, who would be counted as principal masters.

¶ And thou wast burdened: Hitherto his faithfulness in executing his office, now he rehearsed his virtue against external evils: which were many and great, both of that city and of all the Christian world. The battles of Paul against beasts at Ephesus are famous: 1 Cor. 15:32. But what tranquility could be to the following angels, who should have to do with grievous wolves not sparing the flock: Acts 20:29‑30. It was therefore the commendation of this angel, that he did sustain and endure calamity stoutly, which is declared in a triple degree: that he bear the burden; that he laboured under the burden, and yet was not tired; as though he should say, a great weight indeed of trouble did lie upon thee, under the burden whereof thou groaned, yet thou wast not discouraged that thou shouldst pluck thy neck from the yoke, and betray the truth. It is a manly fortitude to bear troubles and torment. Many bear the yoke cheerfully as long as they feel but a little grief, but to go on constantly among the stings of grief and sorrow is a point of great courage and of heavenly fortitude.

Such was this angel, such also was the whole primitive church. Nero and Domitian had greatly persecuted the church before John wrote these things. And besides Nero and Domitian, it abode patiently under Trajan, Adrian, Antoninus, Severus, Diocletian. The times were never more miserable when the emperors let their labor be hired by the devil to shed Christian blood, which he always thirsts after. Yet the faithful revolted not but continued constantly to the end, becoming at length conquerors, setting up the sign of victory against the devil and all foes.

For what other thing were so many scars and prints, with which many Bishops were marked, who after the tempest of tyrannical persecution driven away, did meet in the Nicene Council, than so many triumphant bows of the victory gotten against the enemies? Paulus Neocesariensis was bereft of the use of both his hands, the sinews being shrunk and cut by the persecutors with a hot iron. Others had both their eyes put out. Others their right hands cut off by the elbow, among which was Paphnutius Aegyptius. In sum a man might have seen a company of famous and picked Martyrs gathered together: Theod. book 1. chap. 7. He was an Angel of an invincible courage, whom so many calamities could not break, yea not bow never so little. Now therefore if we shall gather all these things into one sum, we shall see a most beautiful image of any excellent Church. For behold an Angel sparing no trouble of his own in the labour of teaching, administering the discipline most religiously: suffering none that should offend the Church with his naughtiness: either keeping far away the leaven of heretics, or taking it away most carefully at the very first. And last of all for all these things undergoing boldly whatsoever the wicked enemies were able to inflict upon him. Doth he in any thing need amending? In nothing indeed, if only he had continued in his integrity: but godliness fainteth by little and little unless it be kindled continually: and oftentimes a certain naked profession remain, where all his power is utterly dead & lieth quenched: as we shall see by & by to have happened here.

Referring to the words, Montanus and the vulgar translation distinguish this verse differently, and they also omit and change some words: And have borne a burden and have patience for my name, and have not fainted: So, Aretas, but the first words are set out of order: And have patience and have borne a burden. But these readings lack expressive meaning, which our books have, that conjoin together burden, trouble, and perseverance. The sentence becomes much weaker where the word “trouble” is omitted.

4 But I have somewhat against them Hitherto was the praise: The reprimand is for the leaving of their first love: Of which even a light slacking had not wanted great fault: But to put off the same wholly, how great wickedness: For so the word thou hast left, soundeth: as if the Ephesians angels were like to those widows given to riot, which Paul says, are to be condemned, because they have cast away their first faith, 1 Tim. 5.12. Although this loss of love was nothing to the heinous offence of the widows, For their Apostasy was manifest, his only a faint, or rather no care, and a very great negligence of godly duties, the profession of the truth being kept. But the Spirit speaketh of divers times, as it appeareth from this that he says, that thou hast left thy first love, and in the verse following biddeth them to do the first works. From which it is perceived easily, of what sort was this coldness, to it that the Angel who in the first times of the Gospel received, faithfully executed the office of teaching, and observed diligently everyone’s manners, to which forthwith he applied a remedy by ecclesiastical discipline: afterward in the latter years did so languish, that he was negligently occupied in the first labour, permitted some of his flock to perish through ignorance, some through the infirmity of the flesh to be carried headlong into destruction, no lawful curing undertaken. This is that love, which Christ takes grievously to be laid aside so shamefully. For he shows that he is then truly loved, when his sheep are fed faithfully and with a sincere mind. Whereto pertains that thrice repeated commandment to Peter, If thou lovest me, feed my sheep, John 16:17. But in process of time in this Church this fervency waxed cold or rather altogether vanished away, as is manifest by the reprimand. Such is our infirmity rushing apace no less to the loss and destruction of spiritual life, than our bodies has continually to the graves. Wherefore then is there too much cure of this, and none of that? The Ephesians retained an outward profession, neither were any calamities able to take it from them, as the former verse even now taught, yet in the mean time they decayed by little and little, neglecting those things, without which true godliness cannot consist. And this leaving of love seems to have come to pass then, when John had been sent away into Patmos. Doubtless while he abode at Ephesus he suffered not either doctrine or discipline to decay, but being at length bereft of so vigilant a watchman, they fell into this detested drowsiness. The bishop may serve as an example, although not of that city, yet of a neighbour place, who through the negligence of holy discipline suffered a certain young man delivered to him by John to be kept, to become a thief and a robber. Wherefore John did worthily hit and cast in his teeth his good keeping: Eusebius Histories book 3.23. But however the history is silent in this matter, it is certain that the Ephesians angels fell together into shameful negligence about these times. Of which sort also we find the carelessness of the Church growing in use by little and little.

In the first times, while the Apostles served as presidents and eyewitnesses of all things, the diligence of the Elders was fervent; they both preached the word of God faithfully and furthered the godliness of their flock carefully by discipline, but after two hundred years from Christ’s birth they suffered as all things worsened, by a manifest decline. How did discipline begin to be loosened and corrupted when the Martyrs and Confessors gave rest to those who had fallen, not only without the Bishops’ counsel but also against their will? How this outrageous disturbance of the heavenly rule troubled Cyprian, we may see from his epistles: among other causes of the incumbent persecution many of which he rehearsed, at length he descends to this, and what plagues and what stripes do we not deserve when not even the Confessors keep discipline, who ought to have been an example to others in good manners? Epist. book 4, §4. And not many years later, Eusebius relating the condition of the Church a little before Diocletian began his persecution says: “They, who were thought to be our Pastors, rejecting the bond of godliness, were busily occupied in mutual contentions among themselves.” These things only increased beyond measure—contentions, threatening, emulations, mutual grudges and hatred—following with all their might the preeminence and dominion, as it were kingdoms. Book 8 of History, chapter 1. It must need be that the edge of holy discipline was made blunt in a wonderful manner, which had no force to cut off such noxious herbs. But Ambrose, who rehearsed that the divine rule had vanished quite away before his times, speaking of the Elders, at length infers most clearly: “Whereupon he says both the Synagogue and afterwards the Church had Elders, without whose counsel nothing was done in the Church.” I do not know by what negligence it has grown out of use unless perhaps by the slothfulness or rather pride of the teachers. He was not long after that time, which we call the Primitive Church. Yet he speaks as though some ages before his time this wholesome custom had been abolished. These things clearly show how in later times the first love waxed cold altogether and at length went to nothing.

5 Remember from where you have fallen; such was their sin: the remedy consists of three parts—a just consideration of their fall, repentance, and redressing of the discipline.
All of these together are required for amendment, in the same order in which they are presented.
Because we fall little by little, we hardly perceive how deep the pit into which we fall: but let us look back to the high point from which we fell, and we shall marvel at the gulf in which we lie.
Whereupon he warns that he knows from where he fell.
It is not enough simply to perceive that we have fallen; we must quickly get out of the gulf through repentance.
He therefore joins repentance: but many deceive themselves, thinking they have repented well when in fact they have done nothing.
Therefore, lastly, he requires that the first works be done.
Then you will prove your repentance just if it brings forth true holiness of works, and either return to the first love if it is sincere, or increase it by adding a greater one.
But why does he require the first works immediately, especially in the Antitype, which covers about three hundred years?
Would he want the Church, which spread far and increased with an innumerable multitude of people, to return again to its cradle?
Or does he want there to be the same reason and respect for the whole earth, which is one city?
Now also it was near when the Church was to have a Christian magistrate, with Constantine about to come straight to the empire and government of the world:
What need would they then have for that former ancient discipline?
It may have been fitting that Christ had waited a little time, and had not urged so earnestly the first beginnings, which would not be useful in the short term.
But these are the dreams of those who are sick with a fever.
He who knows what is most fit for his spouse earnestly requires the first works after so many years, and after the dispersion of his church in many places:
he wishes that she labor again in the word, and that she punish wicked men with ecclesiastical discipline.
He knew that the order appointed by him should fit both provinces and cities: it should not hinder civil administration, but further enhance and adorn it above all.
From hence let us learn that this first government is common to all times and places:
It should not be permitted for men to follow whatever they wish, but in reforming the church we must always have recourse to the first beginnings:
This rule must be recalled whenever something errs from the right way, and it should not be framed according to the corruption of following churches.

¶ Or else I will come against you quickly: The threat spurs and stirs up the feeble strength of the remedy. Often the fear of peril prevails more with men than the hatred of wickedness. He threatens that he will come quickly and remove the candlestick from its place. But what need is there for him to come, who walks in the midst of the candlesticks? He does not dwell among them as an avenger, but as a brother and defender; from whence, as often as he must take punishment, he puts on a new person and form, in which he had not appeared before: and it is said he comes from another place, and seems now another, from him whom they had known before. In Greek it is, “I will come to you,” against you. Now, to remove the candlestick from its place is to take away the truth and dignity of the Church. Which, though not noted expressly by historians, is that according to this combination, Ephesus lost its form and honour as a church for a time. I contend not about the name of a church, which I know she has retained for many ages, but for the first purity, by which alone God measures a holy church, and not by coloured and naked names. Much less is the candlestick to be understood as the episcopal dignity, as the Jesuit would have it, which we read to have continued from those times, at least eight hundred years. Therefore this candlestick was not quickly removed: Did the angel perhaps repent? It is not likely, seeing that in the Antitype it is certain, that something followed in a short time, which is threatened here to come to pass. For the angels proceeding in negligence, as we have learned from those things previously spoken, Christ took the first golden candlestick from men’s sight by taking away his most holy ordinances, of which the world was most unworthy, on which the primitive church was founded by himself and his apostles. For there was a new face of things when Constantine came: there remained yet the desire of preaching among the bishops: but the doctrine was foully contaminated in many points: relics began to be counted, temples were adorned more magnificently, all kinds of superstition increased, besides the pride of the teachers, as Ambrose had taught, spoiling the church of a necessary help to rule their manners. Instead, ecclesiastical dignities increased, all things being sought out more for pomp than for truth. And while men gave themselves to such things, the golden candlestick, which among the candlesticks had obtained the chief praise, was removed from its place. This will be clearer than the light at noon in the rest of the book. In the meantime let men see how evil they provide for themselves and the truth, which they think is everything right, which they read to have been used in those times. Rather let them go to the entire age in which the candlestick stood in its place: after it was set in another place, it was overwhelmed with darkness, and it could not give light to others.

6 But this you have & c. This also avails to quicken their carefulness: they might have been proud of their present happiness, as though their own godliness had procured it for them: It is not so, says the Spirit: but in that the punishment is yet withheld, it does not come from your approved faithfulness and diligence, but from the only mercy of God whereby He spares that little good, which you have yet left. For as He would not have destroyed Sodom if ten good men had been found in it, so His wrath does not grow hot against Him, as long as any hope of good remains in them. It was but a small thing therefore, that let it be, that He should not by and by translate the candlestick, nor should suffer it to remain any longer among them. But what was this small thing? To wit, that He hated the works of the Nicolaitans, that is, of those whose chief author was Nicholas of Antioch, once one of the seven deacons, Act. 6. Who taught that wives ought to be common, and that it was an indifferent thing to commit adultery, as Irenaeus, Theodoret, and others declare. For as touching that Clemens Alexandrinus Strom. book 3. does attribute this heresy rather to the wickedness of His followers, who drew this foul licentiousness, the fact and saying of Nicholas, which had respect only to the removal of jealousy, it seems scarce credible. For John would have spared the credit of the man, and would have told the ringleader of so great filthiness, nor would have suffered his name to have been borne falsely by wicked men. The Ephesian Angel therefore was pure from the contagion of this sin. What were the Angels of the Primitive Church? They were no less free from this blemish. This heresy was soon rejected, for His own foulness. But after we shall see, that the doctrine of the Nicolaitans did extend not only to the filthiness of the body, but also was transferred unto spiritual fornication: ver. 15. Were they also without fault in this part? In the first hundred years the Church remained a chaste virgin: in the next ages it began to wax wanton, defiling somewhat the marriage bed, partly with unprofitable opinions, partly with foolish ceremonies, but somewhat fearfully & privately at first: nothing according to that impudency which came together with Constantine, and afterward. In this respect therefore, Christ suffered it a long time, although He saw that their first love had waxed cold.

7 He that hath an ear &c. An Epiphonetic conclusion common to all the Epistles: wherein he shows that all whatsoever they be ought to hear these admonitions of the Spirit. Properly indeed they belong to the angels, but it concerns us all greatly, of what sort their condition shall be. They either offend or do their duty not for themselves alone, but their condition is joined either with the great good or evil of the whole flock. But what do these things that happened so long ago pertain to us? There is the same disposition of all churches, and of every one severally: whereupon it is very profitable for us, of whatever age, to beware of their evil. Although not everyone will obey these admonitions, but only those whose ears the Spirit opens. For they are called to hear, those who have ears. And therefore we ought not to marvel if we see many contemptibly secure these threats, and think that these praises and reprimands do not belong to them at all. But what is that which he wishes to be heard? That which follows by and by, says the Jesuit, “To him who overcomes, I will give to eat &c.” Forsooth, the Spirit would have the last clause to be heard of all churches, and of all the members of any church, but all that which was before the bishop shall have privately for himself: a witty indeed and trusty exposition. Are not the epistles pronounced universally and inscribed to the churches, Chap. 1.11? Would it not profit them very much to be instructed touching the state of their angels, and to understand what they might require of them by right? They are sent indeed by name to the angels, not that they should keep them close to themselves as mysteries, but that by their means, they might be communicated to the churches, whom the Lord uses as his ambassadors, to speak to his spouse. Which does yet more appear from those that follow. For it does not fit a bishop only which after is written to them from Smyrna, “Behold it shall come to pass that Satan shall cast some of you into prison &c. ver. 10,” or that to them from Thyatira, and to you, I say, and the rest of Thyatira, ver. 24. That I say nothing, that in some of the epistles, the exhortation to hear shuts up the whole matter, as to the church at Thyatira ver. 29. To the church at Sardis chap. 3.6., at Philadelphia, ver. 13., at Laodicea ver. 22. Whereupon if the church be reserved to the epiphonema, she ought to open and shut the ears all at one time. For there follows nothing to be heard.

¶ To him that overcometh, I will give to eat of the tree of life: The reward in every one is fitted to the times: and is one and the same everywhere, Jesus Christ alone. For what greater thing can he give to his elect? Or what thing shall we need, if we do enjoy him? But according to the diverse condition of times he is set before us in a diverse manner. In this Primitive Church he is the tree of life in the midst of the Paradise of God. Why? Because the first state of the spouse, was wholly like to the first happiness of Adam in Paradise: of which that was a certain visible image and figure, restored in the last times on earth, after our so long banishment from thence. For there was a tree of life in the midst of the garden like a shadow: here Jesus Christ born of a Virgin was conversant with us in the midst of mortal men: there all kinds of beautiful plants, most profitable both for sight and for meat: here a copious abundance of all gifts, which belong either to salvation, or to ornament: there one river, but dividing itself from the garden into four heads: here one voice of verity among all the Apostles, but which beginning at Jerusalem, was spread abroad into the four quarters of the world, watering all lands wherever it flows with peace and salvation. What pleasantness was wanting there, that the mind of man can think of? What is not here sufficiently furnished by him at whose administration the Angels themselves are amazed? To wit, that terrible Angel, with a shining sword keeping the way to the tree of life; it is now removed out of his place, and an entrance again is opened into the garden most full of true pleasure. Christ therefore promised that those who shall keep themselves pure from the corruptions of these times, neither shall forsake their first love, shall continue those true citizens of this holy Church, and that they shall have free leave to eat of Christ, that true tree of life in the midst of this new Eden. Many wicked men and heretics at that time, were thrust headlong (as once Adam) out of the Celestial garden, yet with unlike issue and condition. For Adam falling away from the shadow‑like Paradise, by faith in Christ he found an entrance into the true, but these heretics being driven from the heavenly and true, what return can ever be hoped for? Seeing therefore that this is the natural sense of the words, how foully do they err, who do count the Primitive Church an infant, rude and imperfect? and do attribute ripeness of age and perfection to the latter corrupt times? For they do prefer Tophet before Paradise: neither do mind that all pleasantness did belong to the first beginning: but thorns and thistles and all noisome herbs to the curse following. Far be it that we should think the water flowing by dirty channels, either purer or sweeter or fitter for our use, the further it shall be distant from the fountain. Further let the reprobate know that they do never eat of this tree. For there is the same meat both for way and for country: there is only a difference of a more full fruition, wherein we shall rejoice after the battle finished. Neither is the reward of them that overcome given to the slothful cowards. The Angel will keep them far from it with his glittering sword, that they may not pluck anything at any time from this tree.

The Analysis.
So it is the first epistle: the second is sent to the Church of Smyrna, but inscribed in the manner to the angel: afterward he describes the one who sends: that he is the first and last, then that he was recently dead, but now alive, verse 8. The narration partly commends their suffering of affliction, which the blasphemous Jews brought upon them, verse 9. Partly instructs against a new calamity, both showing the author, kind, end, continuance, and also promising a crown, verse 10. The conclusion has both the usual epiphoneme, and also immunity from the second death in verse eleven.

Scholions.
8 AND to the Angel of the Church of Smyrna: Smyrna was a colony of the Ephesians, as we have said. It was also called the Amazon of Smyrna, but the Spirit respects another name. For where it is a sweet‑smelling Smyrna, that is myrrh, far more pleasant than any spices, it is evident that he reproves no fault of this church, but shows that it is most dear to him, however nothing was more contemned and despised by the world. We should not think that it holds the second place after Ephesus. The Spirit does not list the cities by jumps, putting apart Sardis or Philadelphia, or any of the rest, but in the correct order in which they were situated. First, it goes forward to the north, where about three hundred and twentieth furlongs Smyrna is placed on the shore. From there it turns to Pergamum further into the north; from Pergamum the rest, in their order, turn to the south. This order demonstrates the same progress of the church. In our part of the world, the further we go north, the farther we are from the sun, the fountain of light. Therefore, after Ephesus, Smyrna shows that after the first purity the church will proceed each day toward greater darkness, while at length it will come to Pergamum, the final destination; from there it will go toward the south, each day becoming brighter. We will see in what follows that the event so agrees that no equal judge will condemn these things for vain subtleties, but rather, with me, will admire the greatness of the mystery. If we hold back our opinions while the whole matter is fully understood, we will judge far more uprightly, which will be best both for ourselves and for the truth: which I respect (God is witness) and not any desire for division or novelty. But you will say, how is Smyrna’s myrrh so delectable to God, when its condition is worse than that of Ephesus? In outward appearance it indeed is more deformed, shining with no ornament of lawful policy; in this respect the northern corner agrees with it. Yet the fervent desire of the godly, who fought most valiantly for the truth in this miserable deformity, raised to God a sweet savor. Furthermore, the greater the temptation upon them, the more God is inclined to deal favorably with them. He does not then show rigor in threats, but comforts as much as he can, so that he may confirm the languishing and not add affliction to affliction. The Primitive Church suffered the most grievous calamities at the hands of heathen men, which somewhat assuaged their sorrow. But Smyrna must suffer all extremes at the hands of its own. In these griefs, it should not faint or be overcome; he hears nothing but that which may add courage. Hereupon, reprimands are passed over, although it had more of the basest sort than former Ephesus. The Antitype is the next church after the first. Its colony, as of Ephesus Smyrna, sometimes also enjoyed one common name, as did those two cities, because of their great conjunction at first, as Strabo shows. This Antitype begins with Constantine, until which time the Primitive Church, the Ephesian Antitype continued, and proceeds even unto Gratian around the year of the Lord 382 according to Eusebius.

¶ These things he says that he is the first and last: The description of the sender of the Epistle is taken from verse 17 of the former chapter. In these words we have shown that Christ is praised as the maker and ruler of all things, by whose authority and command all things are done, and that to his glory: or rather that in this eulogy the marvelous joining together of his great majesty and his humility is praised. Which interpretation receives confirmation from here, that the condition of the Smyrneans was like: “Thou art afflicted,” he says, “and poor, but in very deed thou art rich.” What other thing is this than, although with the world thou art counted last, thou art nevertheless in truth the first? And together it shows that alteration, whereby the truth first flourished among the Smyrneans in great esteem, afterward despised and trampled under the feet of hypocrites: even as Christ in the beginning was in incomprehensible glory, God with God, but in later times, taking upon himself the form of a servant, made himself of no reputation, becoming like unto men. He takes to himself titles that may fit the present condition of things. Whereupon he spread a diverse beam of his glory in the several Epistles, according to the diverse condition in which the Churches are. Whereby he teaches that his infinite divine majesty is chiefly to be contemplated with the mind, which may be most available for the present matter. But that they should not think that they must always lie in this base estate, he adds another title: Who was, he says, dead, but is alive; as though he should say, “Although I was in the beginning the first, after the last, yet I did not remain long in this most base estate; but death being overcome within the space of three days, I obtained my former dignity, in which I now live forever.” These things then declare the notable change that came to pass at Smyrna, and no less in his Antitype. Where the first truth, which over the span of three hundred years was established by so much blood, became at last to be hated by the Christians themselves, and the last fortune stayed together with his professors: which Christ, having risen from the dead, should rise again from the dust and restore it to its former dignity. Why then should they be discouraged, who their captain has gone before in the same steps? Or why should they fear afflictions, whose outcome is so joyful and comfortable?

9 I know thy works and afflictions: The narration of the condition, which he says, is known to him, as in the rest, lest peradventure they should suppose that their miseries are not regarded by him, because of his long suffering. The state of this Church was afflicted, as at the present time in this verse, so afterward to be expected, in the next: Whereto the Antitype agrees altogether. For after the first age driven away, by and by a lamentable strife arose, when Constantine succeeded. The persecutions of open enemies ceased, but the strifes and contentions of the citizens forthwith waxed very hot. And not only of the whole Church in general, but also of this city: Theodosius Junior boiling with envy against one Cyrus, whom he saw to be very gracious with the people, sent to Smyrna under a color to make him Bishop of this city, but with a determinate purpose that he should be killed; For the Smyrneans had killed long ago four of their bishops; which barbarous cruelty shows how grievously this Angel was afflicted: Epitome chr. set out with Eusebius chr. by the famous Joseph Scaliger, pag. 293. But if we shall enlarge this Smyrna a little unto those contentions of the citizens, of which I spoke; by and by came Arius, who kindled that fire, whereby all things as well divine as human, were inflamed. The Bishops studied no other thing, than that one might spoil another of their seats and dignities. Eustathius Antiochus was banished with a great company of Elders and Deacons: Athanasius in his epistle to them that lead a solitary life. Athanasius himself, the only defender almost of the truth, was not only assailed, but also oppressed with all kinds of false accusations; neither did they cease from their wicked assailing him, before that he was banished to Treveres in France. Those were sorrowful times, when the Emperor, in the meantime, not minding sufficiently the drifts of the bishops, did not know the true original of those stirs.

¶ And thy poverty: That is, how thou art mocked and contemned, as a beggar: but be thou despised more than any of those hypocrites, thou art rich in mine account, that thou mayest regard the wicked’s scoffing of those men as less.
And that we may let pass the Smyrneans, the matter is clear in the Antitype. How few were there of the Orthodox that dared to profess the truth? How superstitiously were those few suppressed by the enemies? Certainly the Saints were constrained to run hither and thither in order that they might seek aid against tyranny. They, too, being turned out of their goods, could not maintain their life except by the liberality of others. Athanasius alone may serve as an example, from whose many perils—flight, hidden places, no hope of escape—anyone may easily see how the faithful could prevail, even with little wealth, against the injuries of their enemies. The Smyrnean angel was then poor indeed, if we measure riches by human defence.

¶ But you are rich: Not naked and forsaken, as men think, but by me, and in my account, abounding in all riches. These things are also together to show what defense and esteem Christ could prepare for him even in spite of the world. Authority increased together with affliction, as we know it came to pass concerning Athanasius, who, being vexed with all manner of contumelies in the East, was esteemed highly in the West. Constantius the son, Constans the brother, Julius Roman, the Bishop of Treveris, who gave him entertainment most kindly and liberally for the space of two years, reverenced him according to his worth. Moreover, Constantine the Great himself, having perceived the calumnies of his adversaries, honored his innocence and virtue, and determined to bring him back from banishment.

¶ And the blasphemy of those &c. Hitherto the kind of the present calamity: now he show the authors, arrogating to themselves, that which in no way was fitting them. But is it blasphemy for a Jew, to profess himself to be a Jew? A Jew is taken figuratively for one people of God, which alone among all men, knew the right way of worshipping him; as though he should say: They that boast that they worship God after the ancient rule of the law, in the manner their ancestors once worshipped, and all men ought always to worship. This was blasphemy, the retaining of the worship abolished, and the thrusting upon God the ancient ceremonies, by which the glory of his son sent at length into the world, should be overwhelmed: For which cause, although they were Jews by stock, they lied in affirming that they were Jews, being so far from that holy people, that in very truth they made a Synagogue of Satan. And it is known, with what bitter minds they persecuted Christians in all places, as we see in Paul & Barnabas at Antioch, Pisidia, Iconium, Lystra, and in other places, Act. 13.50. and 14.2.5.19. Which they did also at Smyrna about these times, as we learn from this place. Under Constantine these Jews were Arian bishops, namely, Eusebius Nicomediensis, Theognis of Chalcedon, Maris, Patrophilus, Ursatius, Valens, and the rest of this sort, men indeed not ethnics, nor wholly void of all knowledge of God, as neither were the Jews, but bearing the name of Christians, & such as were standard bearers in this war. Who notwithstanding did hold their errors with tooth & nail, no less than that stubborn nation of the Jews, striving to establish their Decrees only, to vex by all means such as were contrary minded, to boast that they alone had the true faith, to condemn all the rest of ungodliness and blasphemy. But whatsoever boastings that wicked company made, as though God dwelt in their congregations only, they gathered Churches not to God, but to the Devil, of whose Synagogue, they were the chief rulers.

¶ Fear none of those things which you shall suffer. Now he instructs them against the future evils, which appear to be more grievous than those that have passed. Those things with which the Jews troubled them in the present, and also those false accusations of the bishops while Constantine lived, were minor skirmishes of a sharper battle that followed. Therefore he describes diligently the manner of this combat, who should be its chief captain, how cruelly he should rage, to what end, and for how long. The Prince is the Devil, whom after we shall learn to denote as the heathen emperors, open enemies of the truth, as in chapter 12.9. This also includes the heretics, Christians in name but, in truth, wolves devouring the flock.

The kind of punishment is imprisonment, which, as history teaches, includes prohibitions, confiscation of goods, banishment, slaughter, fire, and torture. With all these measures, the devil would greatly torment people to draw them away from the truth. But this persecution should last only ten days. In this book, one day is taken to represent a year. The number ten sometimes signifies a definite quantity, and sometimes, by synecdoche, points to an uncertain number. I think both are used here: a certain number represents the type, and an uncertain number represents the antitype. Therefore, regarding Smyrna itself, this persecution occurred during the reign of Trajan, when the devil—an enemy of truth—reigned after this writing, was very fierce against Christians, sending men to prison and death, so that he could force them to renounce the profession of Christ.

Smyrna could not be free from the common calamity, especially when Bithynia, being near it, was altogether abounding in the murders of the Christians, as the epistle of Plinius Secundus to Trajan shows. From this, one may also gather a sense of the continuation of the persecution. For in the fourteenth year of Trajan, Pliny, relating to him the multitude of those who were slain, offered an occasion to halt that rage and to obtain some relief. The year it began is not plainly set down by the historians. Some suppose it was at the very beginning of his reign, but in the fourth year, after triumphing over the Dacians and Scythians, he seemed to have had his kingdom first hindered, so he could not afford the leisure to afflict the Christians. But it is certain that he exercised his cruelty for at least ten years. It is likely that the end of that war gave the beginning of the torment of Christians. Neither is it necessary that this affliction be referred to Smyrna only; rather, it was part of the general persecution mentioned in the Church of Philadelphia, which should affect the whole world (Ch. 3.10). As for the Antitype, Constantine and Valens, who were Christians by name, they were no less fierce against the orthodox and true godly people than the ethnic devils once were. In this account, the inferior ministers of that wickedness are also held: of the people, Syrianus, a captain, and Sebastianus, governor of the Manichean armies; of the bishops Eusebius, once of Nicomedia, then of Constantinople, Macedonius, George Alexandrinus, and others of that sort, not bishops but monsters: whose barbarous cruelty was scarcely matched by any tyrant. In old times, the matter was handled with brawls, chidings, and calumnies of all sorts. But after the death of Constantine, the devil came to the fore, and what turmoil was raised? It was a light thing to banish holy men, imprison many, and kill almost an infinite number; they tyrannized with torments and all manner of contumelious punishments. Some were beaten with stripes to death, some were marked on the forehead with prints of hot iron, some were tortured in other ways. Indeed, the breasts were cut off from holy women; some were burned off with a hot iron; many had eggs roasted in a fire at an excessive heat. Who would believe that any such thing could have been inflicted upon Christians by men of the Christian profession? It cannot be shown in a few words how full of calamity those times were; see Socrates, book 2 and 4; Theodoret, book 2 and 4; Sozomen, books 3, 4, and 6.

And although this tyranny continued for more than fourteen years, yet nevertheless it makes those ten days in the same manner that we have said.

¶ Be faithful unto death: He provokes fortitude, the reward being proposed to be eternal life. It is a profitable loss which is recompensed with such great gain. What should the godly not undergo most willingly, being sure of such a reward? It is fitting for the times, ministering comfort against the loss of this present life. To which purpose did he speak before, that he was alive who had been dead, that by his example they should learn not to fear death, which they should know to be a means between God and them to eternal happiness.

11 He who has an ear: the usual conclusion, warning all men, to hearken diligently to these instructions touching fortitude and courage of mind in afflictions. We were instructed before against the sluggishness which is inbred in us: here we are armed against outward violence. The reward which is added to the end, he who overcomes shall not be hurt by the second death, is common to the whole church. That which was before belonged properly to the angel, the knowledge of which, notwithstanding, was very necessary to the people, as has been said before. But seeing that this conflict was to be undergone as well by the people as by the pastors, comfort also is given them by name, to the same purpose that the former was, but in a different respect. For there are two things which are wont to kindle the desire toward every excellent act, hope of reward and contempt of peril: that first was proposed to the pastors, whose courage is wont to be more ready and valiant by looking into the reward. This second to the people, whom the fear of danger chiefly withdraws from their duty, and prevents them from undertaking anything worthy of commendation. He teaches therefore that they must not fear to spend their life, if need be, for the truth’s sake: for there shall be no fear of the second death, by which the body and soul perish forever, according to Christ. Fear not those who kill the body, but cannot kill the soul; fear instead him who can destroy both soul and body in hellfire, Matt. 10:28. This hellfire is the same that he calls the second death: by which the whole man shall be no less deprived of all solace in God, as the body is destitute of all help, being separated from the soul by the first death. This is that horrible death, to be feared indeed, from which he who has overcome death delivers his: from which he promised to free those that overcome. He does not promise to deliver them from the first, being too light a thing, either to be given by such a great price rewarder, or to be expected by those that are his. And what need is there to be defended from the first death, which the necessity of nature will bring at length; but to prevent it for the truth’s sake procure a far greater crown? He promises therefore what is best, and does not allure us with a vain show of some light thing.

Analysis.
So is the Epistle to the Smyrneans: That to the Church of Pergamus is inscribed likewise to the Angel: he that sends has a two‑edged sword. The narration commends his constancy, illustrated by the throne of Satan, and the common times, in which Antipas suffered ver. 13. Then he reproves the sin: which he shows what quality it is, consisting in suffering Balaamites ver. 14. and Nicolaitans ver. 15. and also the remedy for it, namely repentance, which he sets forth by the danger of refusing the same ver. 16. Lastly he concludes with a solemn Epiphoneme, and proposes a reward, the hidden Manna, the white stone, and an unknown name, written upon it, ver. 17.

Scholions.
12 And to the Angel of the Church of Pergamus;* 1.3 Pergamus so far as the Spirit seems to respect the notation of it in this place, is as it were 〈 in non-Latin alphabet 〉, that is, 〈 in non-Latin alphabet 〉 the tower of Troy, as Hesychius expounds it: that is, a towered city, high and superb, agreeable to that which follows in the next verse, where the throne of Satan is. It is distant from Smyrna to the north about five hundred and forty furlongs, with a greater distance than Smyrna is from Ephesus, in the last border of the North latitude as touching those seven cities. A great diminishing of light fell out in the Smyrnean corner under Constantine, Constans & Valens even at the first turning from Ephesus into first purity: But now he goes from Smyrna to Pergamus into the utmost darkness, the Church being about to suffer a greater defect of light than ever before this time since Christ was born. The Antitype of this Church is for longer time than the former, as also the distance of place is greater, containing a great part of the kingdom of darkness, from the three hundred and four score years, that is, from Gratian, where the former period ceased, unto about the year one thousand three hundred, as in the explication we shall see.

¶ These things says he who has etc. The furnishings of those who indict the Epistle are taken out of chapter 1.16. Which he now takes before the others, because he would demonstrate this in practice in this Church. For he would punish the rebels, as he says after verse 16, upon whom no mild punishment should be imposed by a double‑edged sword, for the sword is sharp. The sword is the word of God itself, whose force should now be manifested in subduing the sinful man. Although this sword in this period is shaken rather than inflicted. For he threatens a fight against those who do not repent, verse 16. He does not come immediately with swift blows.

13 I know thy works: A narration of his more approved condition, which is set forth two ways: that he neither denied the faith, although he dwelt in that place where Satan’s throne is: secondly that neither in those days, wherein Antipas was slain. It is not hard to know, why it is called the throne of Satan. For the city where the Ethnic Emperors had their seat made war professedly against the Lamb, is called the Throne of the Dragon, chap. 13.2. So of the foster & inferior cities, which come nearest to the disposition of this chief city, because they make a palace more garnished for the Devil, they are noted with the same name.

Now it was the mother city of the Roman Empire in Asia. For it is likely that this region, being brought into a province, after Attalus Philometor, king of Pergamon, had named the people of Rome his heir, the proconsul was sent to govern the same, placing there the seat of his jurisdiction. Pliny in his fifth book of Natural History, chapter 30, says that this city was by far the most famous in Asia, and its glory should not be less if the proconsuls had dwelt in any other place, seeing that honour is wont to come to cities or depart from them together with the chief rulers. Although before it pertained to the Roman power, it was the head city of the Kingdom of Asia. For so Livy spoke, urging of Seleucus, son of Antiochus; he led, says he, to the assailing of Pergamon, the head and tower of the Kingdom, Decal. 4, book 7. It was therefore a great thing to profess Christ in the hearing and sight of such a mighty city, spiteful against the truth. There may not be prophecy in Bethel, for it is the sanctuary of the king and the king’s house, Amos 7:13. Aretas reports of Antipas, that he gave testimony to the truth at Pergamon, and that his martyrdom was known even in his times: but I find no more in any author worthy of credit. From this place it is evident that he was a very famous martyr, by whose sufferings the rage of a most grievous persecution was signified. This is another praise that Pergamon had continued steadfastly in the faith, when a fierce tempest raged greatly.

It is an easy thing to profess Christ, when a man may do it either with honor, or without danger: but to retain the profession of him without fear, even with the danger of life, is an excellent commendation and a point of true courage. We have said that the Antitype was the Church from the four hundred years, to the three hundred above the thousand; when after Constantius, Julianus and Valens, Smyrna being left it went further toward the North unto Pergamum, that is, was hidden in thick darkness, being brought under the power of that city, where the throne of Satan is, namely Rome.

This is that Towering City, the Tower of Troy, whose daughter she boasted herself as, once the Mother City of almost the whole world, the proud lady and queen of the nations no less famous for the stately temples, theatres, high places, than for the ample and large dominion and empire.

It is plainly called the Throne of Satan in the chapter 13 of this book, both because it was once the Seat of the Ethnic Emperors, as at the place we will show, and also because they being taken away, it was made the Seat of the Popes, who during this time have most plainly shown that they reigned by the help of the Devil and not of God. Four and twenty Popes were all given to Devilish arts: some of which gave up themselves wholly to Satan by covenant to obtain the Popedom. Yea by the space of whole four score years from Sylvester II unto Gregory the seven, no Pope reigned but was greatly famous in this impiety. Can any doubt where the Devil hath his Throne placed, when he shall see so many Necromancers clothed in purple sit at Rome? Rome therefore is Pergamus, and not only the city of Rome, but the whole Roman dominion, as far as the Dominion of the Roman Bishop did extend. As long as this tyranny flourished, in all those places subject unto it, there was the Seat of the Pergamen Church. And they that keep the name of Christ, are the faithful dispersed at that time in every place, who not discouraged with the Roman tyranny, retained firmly in the meantime the sound doctrine, of which sort were many in the East, in Africa, in Britain, and in other places, yet rather apparent or manifest man by man, than notable in any whole assemblies. For now was the time of the Church lying hid, as after shall be showed more fully, chap. 7. and 11. and 12. Antipas was slain, when about the year eight hundred it began to be a matter worthy death, to resist the Roman Bishop. For behold what a most fit name the Spirit gives to the Pergamen Martyr: He is called Antipas not with a feigned, but true name; which yet by almost so many letters & syllables, should declare that the Martyrs of this time should be Antipopes: not that two-headed or three-headed Hydra, whose heads should contend one with another for the Papacy, but who should oppose themselves against these sacrilegious Popes, desiring that the wicked power should be brought into order. Of which sort were Leo Isaurus, killed after a sort by Gregory the 2. when he was by him spoiled of the Empire of the East. Frederick Barbarossa was vexed with all manner of injuries. The Bishop Florentine of less fame, was condemned, for teaching that Antichrist had come. A certain man called Arnulf, or as others write Arnoldus, was hanged at Rome, because he had spoken boldly against the Pope, Cardinals and Priests.

Gerardus and Dulcimus Navarenses were burnt alive with thirty others because they preached that the Pope was the Antichrist, and many others, of whom a catalogue would be too long, are not my purpose.
The godly reader may conjecture from the Decrees, which are found in the Right of Bishops, how many Antipopes, or rather the Antipopes, were killed in this Pergamon state.
The first is: He who goes about to take away the privilege of the Church of Rome, given by the very highest head of all churches, undoubtedly falls into heresy and is to be called a heretic, Dist. 22.
All or the Patriarchs again, let him become anathema with God, which violates the censure of the Roman Bishops, cause 25. q. 1. general decree.
To which add, they are not homicide, who through zeal of the mother Church are armed against excommunicates, cause 23. q. 5. Of the killers of excommunicates.
From this consider yourself, seeing the good will of the Roman Church has always been the same, even before these laws were made, how many Antipopes have been killed of the same, after she had obtained some power.
Yet many, even in those times, kept the truth faithfully, as far as it was revealed to them, for which cause a more glorious crown is laid up for them.

14 But I have a few objections to you: The other part of the narration, wherein the angel is reproved for his excessive gentleness toward the wicked. From where it came to pass that this Church was infected with the doctrine of Balaam in this verse, and the Nicolaitans in the next. There was but one plague of the Nicolaitans in the Church of Ephesus, to this is also added Balaam. Whose fornication (which he taught) had not respect so much to the defiling of the body as to the violating of godliness by idolatry. Which double corruption is so distinguished that the doctrine of Balaam is proper to the antype, although it be rehearsed in the former place, the doctrine of the Nicolaitans to the type, to wit of the very city Pergamus. As touching that, most fitly is the pope of Rome in those first times compared to Balaam of great authority with kings, ready for any thing for the sake of profit, uttering some true oracles, but as a diviner and man of ethnic superstition, persuading the worship of images to Constantine and Irene Augustes, as it may be seen in the synodical epistle sent unto them, as Balaam to the king Balak, that he would entice the Israelites, beautiful women being set before them, to offer sacrifices to Baal Peor, Num. 31.16. Now therefore we see why Balaam was reserved to this place, to wit, that he might signify his true offspring, the pope of Rome, as like his father, as one egg another. He in these times which we have spoken of should tread the church under feet. But this was the sin of the Pergamian angel, that he suffered too favourably men to draw of the dregs of this false prophet. It was his duty to have been instant in teaching, admonishing, reproving, correcting, if peradventure the contagion might have been stayed, that it should not spread further abroad. Of which when the godly were something too negligent, handling too gently this man of sin, and halting or somewhat failing, as comes to pass in a common corruption, gave occasion to the overseer of churches, both to contend with them, and also at length to punish that estate. And who knows not how tenderly and mildly they which embraced the truth in those times touched in speaking or writing the Roman tyranny? They should have thundered against it most vehemently, and spared no sharpness of words, but we shall find that the angel in this point performed not his duty. But how then had he but a few things against the angel, seeing the whole state of the church was so greatly corrupt? Wonderful is the gentle entreating of our God. He requires but a few things of them to whom he gives few. The greater their corruption was, so much the less he exacts. He requires not so great ability of him that lives in darkness as of them around whom the clear light shines.

¶ That they should eat of those things which were sacrificed to idols; that is, being present at the worship of idols, should give honour to them. Otherwise, if anything offered to idols were sold in the market, and the offence of some weak brother was not hindered, anyone might well eat of it, 1 Cor. 8. &c. But the spirit seems, with good advice, to have spoken rather of eating that which is offered to idols than of worshipping the idol, that he might show the crafty and subtle ways of this Balaam in provoking and alluring men to idolatry. It seems not so ungodly a thing for men to eat flesh sacrificed to idols as to fall down at their feet and give adoration to the image. Therefore this Balaam would endeavour to win men to his purpose by very small things and having a fair appearance. He would abhor idols in words as much as anyone else, and would cry out that the honour he commands to be given to images is far from this ungodliness, by such words deceiving the unskilled and bringing them into this offence, which the spirit speaks of.

15 So you have, etc. The reduction of the similarity, whose proposition has not spoken a word of. Thus it should be full. As once the Israelites had those who held the doctrine of Balaam: so you have those who hold the doctrine of the Nicolaitans. Instead of the proposition, he attributes the doctrine of Balaam to the Pergamon Church, because it was proper to his antitype: but from where may be gathered the first part of the similarity. But this poison of the Nicolaitans had infected undoubtedly Pergamon.

¶ Which I hate: as before, the common translation is, repent likewise. And so he begins the verse following in this sense, as I have warned the Ephesian Church, so do I admonish thee. But this is weaker than if he did command simply, repent.

16 I will come against you quickly, and fight against them; He threatens a double punishment, one against the Church itself against which he says that he will come quickly: The other against the corrupters, against whom he says he will fight with the sword of his mouth. For we may not think, that he will come against the Church, only to take away those plagues and destructions of men (for this could have no fear, but would be a thing to be chiefly wished) but she also must suffer the punishment of her negligence, as well as their wickedness. Therefore this violent breaking into the Church, was a certain chastisement by war, or some such calamity, as is manifest in the Antitype: whose times were very troublesome, partly by the overflowing of the Northern Barbarians, partly by the Saracens, whom the Devil armed against the seed of the woman, after she fled into the wilderness, as we shall show at the chap. 12. to which times these things pertain: but here generally and obscurely shown, because this place suffered not any ample light. The other punishment is against the Balaamites, against whom he will use the sword of his mouth. For we must observe, how he distinguishes these from the Church: of her he said, I will come against you, then turning his speech to the Balaamites, and I will fight, says he, against them. But what is it to fight with the sword of his mouth? Whether to inflict the punishments which he has threatened in his word? Certainly Paul says that he had in readiness, wherewith to punish all defiance, 2 Cor. 10.6. And Jeremiah is set of God over the nations and Kingdoms, to root out and destroy &c. chap. 1.10. For there is no weapon in the whole armory of the world so effectual on both parts. Wherefore seeing by the judgement hereof all fornications and idolatry are appointed to a just punishment, worthily may he say, that he will fight with that sword, according to the rule whereof the pronounced judgement is exercised. But now when in another place it is said of Antichrist, that Christ shall consume him with the spirit of his mouth, 2 Thes. 2.8. (which manner of speaking what force it hath, we have learned by experience, to wit, that his errors convinced, his lies detected, then his fraud and deceits set in the open light, he shall be brought to destruction) these words seem to have the same meaning. And certainly after that the Church was for a while scourged by those Northern & Southern barbarians, Christ began to vex those Pergamen impostors with the light of the truth: for about the year 1120, arose certain godly men, which preached openly that Antichrist was come: that the holy days, Ecclesiastical broken songs, prayers for the dead, pilgrimages, oil, extreme unction, & the rest of that sort, were superstitious things: Work Trip. & Henric. Mon. Thol. To these were added in a short time after the Waldenses, the Albigenses & Parisienses, who published a book of the perils of the Church, & many other private men. From thence began this fight, which was soft in the beginning, terrible rather in the shaking of the sword, than in wounding: but after coming to a just & full battle, as after we shall see, which hath fallen out prosperously to the godly hitherto by the grace of God: but most unhappily to them that dwell at Rome in the throne of Satan.

17 He that hath an ear; let every one drowned in the Roman superstitions give ear, let him attend and hearken, in what account with God is that unmarried vicar of Christ: of what price is that famous and much spoken of Rome, that Chair of Peter, the pillar of truth, mother of the faith and of all churches; to wit, that chief prelate, that wicked Balaam: the very city which is renowned for the vain praise of men, the gate of heaven, is the very palace and throne of the Devil. Neither let anyone think that hatred does wring these words from a man who is an adversary: but let him compare the prophecy and the event, which if he sees that they agree in all things, let him know that he is warned of danger, not so much by the words of men as by the Holy Spirit.

¶ To him that overcomes I will and so on. The reward is threefold: hidden Manna, a white stone, and an unknown name written upon it. Each fits the times in a wonderful manner. As for Manna, it is the meat of the wilderness ministered by God when there was no means to have other bread. In this Pergamen state, when the company of the Nicolaitans and Balaamite offspring, that is, Roman idolatrous, possessed all places, the Church was conversant in a waste, unpleasant, and terrible wilderness, whither we shall see the woman betake herself flying from the Dragon, ch. 12. But Christ feeds the same with the meat of the wilderness, as once the Israelites. For he will not be wanting to him in the most difficult times, but bestow abundantly the joy of the Spirit, whereby not only may they be preserved in life, but also be very glad for the greatest joys. Therefore this Manna is the same meat, with the fruit of the tree of life in Paradise, as has been observed afore, ver. 7. but the manner of ministering it is different; there, in a most chaste, pure, and flourishing church, it was the fruit of the tree in the midst of the Paradise of God: here the truth being despised, contemned, and trampled underfoot, and utterly oppressed with thick darkness, it is Manna the food of the wilderness: this meat should be hidden from the world, and they should suppose them famished, who had fled into this wilderness, as the Egyptians thought the Israelites for this cause would perish suddenly. But God did sustain him extraordinarily with this bread of Angels.

Yet there is this difference between the manna of the Pergamen people and that of the Israelites: for this every way was spread round about the tents, that was dispersed peculiarly to every one of the saints, who did not dwell so close together in such great numbers as the Israelites in their tents; but in certain remote dens, far from the eyes of the world. From where the manna of these is hidden, theirs is manifest, like that which was gathered from the common provision of the people and, by God’s command, laid up in a golden pot, which the people could not see afterwards (Exodus 16:33‑34; Hebrews 9:4). Which, in a more excellent figure, shadowed the heavenly food. For the other manna, kept for only one day, was full of worms; this abode is pure and incorrupt through all ages, a lively and expressive image of the immortal food. Therefore this manna does not lie openly about the tents, in the way that every one who will gather it up, but is given from the golden pot, as much as may be sufficient to sustain life. And certainly, unless Christ, by hidden means, had provided for them in those most corrupt times, they would have been utterly undone with respect to their salvation.

¶ And I will give him a white stone: The second reward. Aretas reports that such a stone was wont to be given to master wrestlers striving in the theater. But that custom is not here regarded: For that was only for the entering of the fight, and not for the rewarding of the overcomer. In the plays called Olympiques, that the champions should not run together rashly, they pulled stones out of a silver pot, and those on which they did fall being marked with the same letter (for they were two by two marked with the same characters) were committed in the fight by the judges: neither do I think that there was any other use of stones in plays. In judgments they were used to another end, to wit to give voices. In which thing they were diverse, according to the sundry laws of the peoples; sometimes hollow and bored through, by which they did condemn, sometimes full and solid, by which they did absolve. Sometimes also they were distinguished only by the colour, the black condemning, the white contrariwise absolving. So Ulpian on Demosthenes against Timocrate: The stones sometimes bored and not bored: sometimes black and white. To the same purpose the Scholiast of Aristophanes in 〈 in non-Latin alphabet 〉. But that of Alcibiades is famous, who in the judgment of life and death would not believe his mother, lest peradventure she unaware should put a black stone for a white, Plutarch in Apology of the King. He alludes therefore to that manner of absolving in judgments. But why now is there a second, yea a third reward, which in the former Churches was but one? The use of the godly did so require.

For, because those few and rare faithful, in so great a multitude of the ungodly, were hated by all, condemned for schism, error, heresy, and I know not what wickedness, an absolving stone is promised to them. Though they might be judged guilty by the votes of all men on earth, yet they may know most surely that they are judged innocent before the heavenly tribunal. How great a solace is this against the reproaches of the world? Be of good courage; if God justifies, who shall condemn? Rom. 8.33.

¶ And in the stone a new name written: A third reward. He persists in the same custom of judgments: in some of which their names were written in the stones, who came to be judged. Aristides being desired by an unlearned one who knew not who he was, that he would write to him the name of Aristides in his shell, he wrote his name into his own banishment: Plutarch in Apology of Aristides. Here the like custom is showed. But the new name to be written in the white stone is the child of God, such as the faithful perceive and acknowledge themselves to be by the testimony of the Spirit, Romans 8:16. Which also avails against the railings of the world, to whom they should be as the filth and offscouring of all. But why dost thou vex thyself with thought of so great contempt, seeing thou art with God in the honor of a son? This name also is unknown to all, except to him that receives it. For the world knows us not, 1 John 3:2. Therefore their testimony is of no account, on what side so ever. But besides behold the solitariness of those times, wherein the elect were no less unknown to the world, than the way of salvation signified now by the hidden Manna.

Analysis.
Such is the Epistle to the Church of Pergamus, 1.4. This to the Thyatirens is titled also to the Angel: then he declares that he who sends is the son of God, with fiery eyes, and feet like fine brass, v. 18. The narration praises the increase of godliness, v. 19, but reprimands for the suffering of Jezebel; whose immorality he describes first by the kind of sin v. 20, secondly by the hardening v. 21, and punishment, which is notable both for the nature of the punishment itself, which is diverse according to the manner of the delinquents: For Jezebel herself is punished by the bed: those that commit fornication with her, by great affliction v. 22, and her sons with death, as also by an excellent testimony of all churches, of the just and severe judgment of God v. 23. To whom finally he annexed counsel against this wickedness (the way where he shows by gentle entreaty, laying no other burden upon them v. 24.) requiring constancy, v. 25, & persuading thereto by the reward of power over the nations, v. 26‑27, & the morning star v. 28. The conclusion v. 29.

Scholions.
18 And to the Angel of the Church of Thyatira: Thyatira is so called as it were Thugatera, as we have shown at the first chapter. A name well concurrent with the thing. For the godliness of this Church is growing, as a newborn daughter, which always grows up, until she has attained full maturity. In which respect it is opposed to Ephesus: which being of full age the very first day, or shortly after, the further she proceeds, hastening to old age, became weaker every day, while finally the natural heat being extinguished, she fell into the cold of death. And here is the first bend from the North, to wit, Pergamus, toward the south, but further to the East, being distant, according to Ptolemy, about eighty English miles. The Antitype is the time from the year 1300 to 1520.

¶ These things say the son of God: Now Christ makes himself known by his name, eyes, & feet: every one of which do appear more clearly from the Antithesis of what sort they are.
Regarding the name, now first of all it offers itself, not expressed before either in the things seen or heard in the first chapter.
There was mention of the son of man, verse 13. but the whole vision did declare sufficiently that he was the son of God.
It seems here to be used, as though now he would return out of Egypt.
He had been exiled for a good while, but in the renewing of the Church he returns as it were home, beginning more familiarly to be known to his, from whom he had seemed before time to be far off.
The fiery eyes are those spoken of in the first chapter fourteen and fifteen verses: by whose clearness he shows to the Theatines, that now the time flourishes wherein the light of the truth should dispel darkness of errors and falsehood, as it flies at the sight of the fire: as came to pass about the year 1300. when a new company of Teachers arose, by the judgment of all which the Pope was strangled, and began to be spoiled of his estimation, which he had kept for a good while by fraud. For they did maintain earnestly, that the Imperial Majesty ought to be preferred above others, and that the Pope had no power over it. Among these were Ockham, Marsilius, Patavinus, Dante, John de Ganduno, and many other.

The feet like fine brass do teach, with what kind of torment the Roman Balaam should rage against the faithful feet of Christ, he should deliver them to be burned in the flame, endeavoring to quench one burning with another.

Which cruelty he has not exercised this first time, but has brought it to noble infamy, by more frequent burnings than ever before. The fires shone through all of Europe; many martyrs were burned every day. But notably before others were John Hus and Jerome of Prague, who, a noble pair of feet like fine brass, did shine in the furnace of Constance in the eyes of all our world. But Antichrist was deceived, thinking he had consumed those feet by fire. Finally, he had experience that these feet are not stubble, but fine brass, which shines more in the fire, and is not consumed.

19 I know your works: The works which are rehearsed, Charity, Ministry, Faith, and Patience pertain to private duty, rather than public office: as though this church were hidden among secret members, and was not renowned for excellent administration. Such was undoubtedly the state of the Thyatirian city: It is plainly related to the Antitype. For although there were everywhere many excellent men, who defended the truth by writings and lively voices, yet no public church companies were constituted or set in order. Or if any were, as about the end of this period men began to meet together somewhat boldly, they obtained no lawful reform.

The chief praise was of their love for one another, not feigned; whereby men promised much but performed nothing, while both by deed and work they helped where there was need, and whereupon they joined charity and ministry. Their mutual faith was also excellent, free from all feigning and treachery. This faith seems to be a fruit of that which is properly called faithfulness, whereby they regarded each other’s goods from the heart. When it signifies a trust in God for Christ’s sake, it tends to be set in the first place, as the fountain and wellspring of other virtues; which perhaps deceived the old interpreter, and caused him to set this word before the other, contrary to the truth of the Greek copies. For so he read: Faith, Love, Service, and Patience. Patience was seen in enduring the calamities that they faced continually due to the hatred and plotting of the Roman prelate.

The last praise is for their last works, which are greater than the former. For so does the Common translation, the Complutensian Edition, and the King’s Edition, which are also used by Robert Stephens in his edition, state: and your last works are more than the first, that is, by presenting the second and.

And so indeed the sentence runs better; especially seeing works are rehearsed at the beginning of the verse: which if they were set down again, and not read together, perhaps the repetition should be superfluous. As touching the matter, it is an excellent praise to grow in godliness, and to exceed the former times in the fruitfulness of good works: which thing indeed befalls them that are planted in the house of the Lord, which in old age are fat and green, Psalm 92:15. Whose way shines as the light, it shines more and more toward the perfect day, Proverbs 4:18. So this Church continues to increase and proceed further and further, growing stronger every day from small beginnings. About the year 1300, many strong, courageous men sprang up, faithful defenders of the truth, but about seventy years later, John Wycliffe added much to their work: he clarified the doctrine in many more points and provided more plentiful arguments, which they had barely found. And forty years later followed John Hus and Jerome of Prague: their preaching and martyrdom greatly increased their influence. The Bohemians followed these, who openly fell away from the Roman Church, and appointed a more reformed worship in their assemblies. And then the minds of all the godly became stouter across Europe, who more boldly professed the truth, however they knew, that they did so at the risk of their lives. Neither did Thyatira stand still here, but about the year 1500, she produced a great number of learned men: who gave no vain hope of a fuller and clearer light that would break forth later. And these are the last works more than the first. Worthily therefore she is Thugateira that is, a daughter growing so notably, even as the waters running from the Temple, which at first was small, then full of shallow places, and could not at last be surpassed by the depth, Ezekiel 47. And so in this first movement from the North created the first pair of contraries; Thyatira grows directly opposite Languishing Ephesus, which has become an omission, leaving, as we have shown, worse in recent times, due to the continual omission of labor and watchfulness, and also by piling up superstitions. Until at last all care of true godliness was abated, and so in the two following Churches it became always worse. Now at last it began to return and to oppose three other Churches, as we shall see in each of them.

20 But I have a few things against thee: The reprehension is, that the woman Jezebel was permitted to deceive the servants of God with her vain shows, Therefore either their negligence, or faint heart, or both are blamed; whereby it came to pass, that she dealt not with the wicked according to their deserts; but they were suffered to sleep securely in their sins. Who this Jezebel was in the Thyatira City, the old History shows not. From this place we understand, that in the same place there was a certain Chief and famous woman, an Idolatress, Sorceress & Harlot, like the ancient Jezebel, which was the wife of Ahab; yet by thus much more furnished to destroy, because this showed herself openly an enemy and adversary to the truth: that would be accounted for a Prophetess. From that which follows, appears that she was taught to the naughtiness in the school of the Nicolaitans, of which she became a school mistress, teaching others the same rules. For the Heretics abused the labour of women to spread abroad their poisons. Simon Magus has his Helena, Carpocrates his Marcellina, Apelles his Philumena, Montanus later in the latter times, in places near to this Thyatira, his Priscilla & Maximilla. In the Antitype the thing is clearer. For this Jezebel is Rome Queen, Idolatress, Sorceress, Whore, Killer of Martyrs, Prophetess, the head of all Churches, and the whole way of salvation, which never yielded to any heresies, and many such like, with which we shall see her adorned by the Holy Spirit partly in this book, partly she boastingly sets forth herself impudently. Lately we learned that the Pope was signified by Balaam, now we have the city shown by Jezebel. Both which pertain to the description of the same Synagogue of Satan, see in the Bishop and the City, are things very nearly conjoined. And how doth it fit the times, that the Spirit doth set before our eyes now such a city? How long did the Pope deceive under a show of godliness, as the Hypocritical Balaam in the former ages about the beginning of increasing honour and reputation? but after he was grown to an immeasurable greatness, lifted up above Kings & Emperors, so as now all men quaked at the very name of the Pope of Rome, his Rome became the Queen Jezebel, an impudent and painted whore. Balaam therefore and Jezebel declare the same kind of impiety: only they are distinguished by the increase and times. Rome in her infancy, as Balaam, handled her matters more warily and secretly: she pretended that she could not speak, but that which the Lord should put in her mouth: being grown to full age, as the Prophetess Jezebel preaches openly that she cannot err, and that she is the rule of faith and all godliness; That abuses the labour of Kings to bring in and set up Idolatry: This by her own authority commands to commit fornication and to eat things sacrificed to Idols, in worship of Idols & Images. Who can admire enough the singular art of the Spirit, who has so lively set forth this matter. This then is Jezebel: the holy men of this time shaking too softly & modestly this pest, have therein so much the less approved themselves to Christ our head, who would have no earnestness spared in repressing so great impudency. Learned men have dealt somewhat more boldly and freely, than they had done in former times: yet they used not that earnestness that met in a cause of this sort.

¶ And I gave her time to repent: In these words is shown the stubbornness of Jezebel. Christ dealt some while patiently with that impure Thyatira woman: so also with the city of Rome, the stormy trouble of Barbarians being quieted, and the Lombards being overthrown. Nevertheless this peace brought no amendment, but increased rather the apostasy, while they came to this height of impudent Jezebel. For we shall see that after those times all ungodliness did grow, the Papists striving to oppress the former dimness with infernal darkness.

22 Behold I will cast her in a bed: The punishment of Jezebel. The bed is sometimes to delights and riot, as in the Prophet, sitting down on beds of ivory, and abounding upon their heads: Amos 6.4. Sometime to sickness and weakness, as, The Lord will uphold him on the bed of feebleness, and turn all his bed in his sickness: Psal. 41.4. Of which in this place? Not of delights, although this be a great punishment, to be given up to the occasion of sinning: but of grief, as appears from this, that by and by after follows, where they that commit adultery with her, shall be cast into great affliction. Therefore the Thyatira woman hath languished. Rome also hath been sick since the year 1300 consuming more every day, as being sick of a consumption. For since that time paleness hath covered her face, her stomach is grown weaker, her soul has become heavy, & her flesh consumed: yea her infirmity hath grown so far, that if thou behold her at this day, thou wilt say that she is a dry carcass in respect of her former plight and good liking. O the infinite wisdom of God, which even in one word, hath given so lively image and picture of a time so far off. Could the languishing destruction of Rome be noted out more elegantly and evidently? God would not have her perish on a swift or speedy disease, that the peoples should not forget her, but with a wasting consumption to be corrupted and wax rotten, both to the end that her lingering punishment should be an image of the eternal pain, and also that she might be a spectacle to many ages, whom she had led in error so long a time. Certainly unless Rome does feel and acknowledge this her consumption, she must needs be sick, not only of a consumption, but also of a phrenia.

¶ And those that commit adultery with her: The punishment of the adulterers, who are the Kings and Princes of the earth, as is after in the 17th chapter 2. Unless these shall forsake the whore, they shall feel great affliction. Have not yet the Kings learned this sufficiently by experience, the most fierce and savage Turk on the one side vexing the Emperor, the Spaniard on the other side? Remember the ages past since the year 1300, in which Jezebel began to languish: Who can attain to declare the great evils which Transylvania, Poland, Bohemia, the House of Austria, the Emperor, the Venetians, the Spaniards, have suffered at the hands of this barbarous Turk? Did not this your affliction begin at the same time, wherein Jezebel in Rome was cast into this her sick bed? Why do ye not observe that your adultery, which this whore hath brought forth, and caused all these evils unto you? But this calamity hitherto, while Jezebel lies sick in bed, is nothing to that wherewith at length ye shall be punished, unless ye renounce betime her ungodly commerce and society, when she shall yield her last breathing, as we shall show afterward. Is it then now time of ye Princes and Peers, to fly like cowards from the true God unto the whore of Rome? They have no pardon or excuse, who bewitched with her beauty while she flourished, accompanied with her. What torment await your wretched lust, who do now embrace a stinking carcass? For the love of Christ provide for yourselves in forsaking with all speed this harlot, lest suddenly at length ye be overwhelmed (when your repentance shall be too late) both with the most grievous calamities of this life, and also those that shall be endless.

23 And I will kill her children by death: the third punishment is directed at her children. These are the Popes, Cardinals, Archbishops, Bishops, Priests, Jesuits, and the rest of the whole troop of this hierarchy. Christ will destroy all those by death, not only in this first punishment, but also unless they repent, in the second. This has yet to come, having begun a long time ago, but will now soon be accomplished, as will be declared.

And all the churches shall know; the churches’ testimony of the just and severe judgment of God. For at length the other multitude of Christians shall have experience that Christ is such a one, as he has declared himself always in his word. His long patience has almost taken away credit from his holy threatenings, but in very deed he shall show at length, that they were not vain terrors of words, but which shall bring most certain vengeance in their time: and this partly begun, partly is yet to come. What reformed churches does not see the long continued languishing of Rome, and praise the just God and celebrate him, crying out, O the depth of his judgments? But there shall be a more plentiful argument of his praise, in his last and full destruction.

And whereas he says that he searches the reins and hearts, in the same he shows to what end his eyes were like a flame of fire, ver. 18. To wit, because not only his servants should approve themselves to be sharp‑sighted in searching out the deceits of this whore, but also Christ should show himself such in administering of things, laying open the impiety of Rome, however coloured with many coverings.

24 And to you I say and the rest: Now he comes to the Council, as we have noted in the Analysis, teaching how they should defend themselves against this wickedness of Jezebel. And it is given to you and the rest of Thyatira, that is, to you the Angel with the company of your colleagues, and the rest of the Church which have abounded in sound doctrine, as Theod. Beza has expounded very well. The common translations, the Complutensian Edition, and others put out the particle and, but to you I say the rest of Thyatira: But Aretas does read the same, with whom other written copies agree. From which particle it is evident that not only the last clause pertains to the Church, but also the whole narration, although it respects chiefly the Angel and speaks to him by name. The same judgment is to be held of the rest, for there is the same reason for each one.

¶ And who have not known the depths of Satan, as they say: But who are they which say? As far as seems to me, the teachers of this heinous wickedness: as though they should brag that they alone did know the depths of Satan, to perceive all his cunning and subtleties, and together also to know the way whereby they may resist his mischievous devices, and therefore that they permitted confused lust and buggery, or at least whoredom, to avoid a greater evil: that the other teachers which the common sort hold true ministers are simple men and unskilled, altogether ignorant of Satan’s enterprises. The name of Satan seems not to be cast in their teeth by John in reproach, but to have been used of themselves willingly, in that sense which I have said. So ungodliness is wont to vaunt itself, challenging to herself alone the power to loose and deliver others, when herself is on every side bound with the snares of the Devil.

Wherefore the Greek word is more fittingly translated by the old interpreter, who have not known. For the Spirit does rather check the boasting of the wicked than praise the integrity of the faithful.

¶ I will lay no other burden upon you; that is, I will denounce no more grievous thing against you, as well as expound it, Theod Beza. A burdensome prophecy was wont to be called massa, that is a burden. These words then show that no notable calamity should invade this church, which ought to be believed to have fallen out in the city of Thyatira. We know that it has come to pass in our part of the world, there having happened no other notable mutation, besides that which was spoken, from the year 1300, in the span of 200 years after and somewhat more. For from that time the Turk waxed strong, but this pertained to the affliction of kings who committed adultery with the whore, as we have shown at verse 22. The true church gets no great loss thereby, but it is a grief to hear that men of Christian name should be trod underfoot so cruelly by a most wicked enemy. Otherwise, while the Turk vexed the Roman whore and her adulterers, the truth springing up again had the chance to grow.

25 Yet that which you have, hold till I come: He exhorts you to constancy, that you keep faithfully the things obtained. Neither is this exhortation only a precept of what you ought to do, but a prophecy of what should be done, as often elsewhere. Therefore you should go forward in the light of truth, neither should you allow yourself to be driven from the right way. And the coming of which he speaks is a fuller reformation, whereby Christ is banished from us while superstitions and errors reign, and when they are taken away, he comes to us, giving us the comfort of his presence. Therefore this glimmer of truth should continue alive, until at last it breaks out into a flame, for instance even in the times of Luther, as we shall see.

26 For if anyone shall overcome, and he who overcomes and keeps to the end, my works I will give to him, instead of “and to him who overcomes and keeps I will give, …”, an Hebraism such as is also in the following chapter, verse 12:21, where the nominative case is put absolutely by defect of the preposition “lamech”, as in Psalm 11:4. Jehovah, in heaven, is His seat: that is, of Jehovah, or as touching Jehovah, His seat is in heaven. So Psalm 18:31, God Himself, His way is upright, for Leel Deo, that is for God, or, as touching God: that of Paul is like, etc. Rom. 8:3, which doth so trouble the interpreters, not marking this Hebraism, whether to adunatum be the nominative absolute, the sense whereof is, for as touching the impossibility etc. But the end which he here mentions is not of this life, but of this period; which should then cease when a perfecter reformation should come.

¶ I will give him power over the nations: the reward is double—power over the nations and the morning star. We have said that rewards are applied to the times and signify those good things that the saints enjoy in this life, while also being pledges of future things. Power over the nations is power over the enemies of the Church. This name once shone upon all, as many were not the people of Israel but strangers to their laws and covenant; now, of the Gentiles themselves, all who profess Christ sincerely are counted among the Israelites. The other multitude, which openly despises the truth or embraces it only in name, remains stuck in their former mire and is called by the old name of Gentiles. There were therefore Gentiles among the Thyatirans, namely Jezebel with hers. Among us Rome with her adulterers and children. Neither must we doubt that the Thyatirans obtained victory against Jezebel, as ours against Rome and her followers. When Luther arose, some princes of Germany departed from the service of the Roman whore; after some struggle they cast her to the ground and trod her underfoot. The same happened by the grace of God in many other places. Therefore this promised power is the society of victory against Papists, which all reformed churches enjoy today. In short, there shall be a full triumph in its place; by God’s help we shall show it.

27 And he shall rule them etc. These are the attributes of the former power. To rule with a rod of iron is mightily to subdue and to compel obedience; they will not. Which was done by the Protestant Prince in Germany and elsewhere, who turned the Papists out of their monasteries, colleges, temples, grounds, and other goods, and bestowed them on former uses, to wit, to maintain godly teachers, widows, orphans, schools, or finally on whatever could be used to promote Christianity. But the Papist cries out that this is sacrilegious and tyrannical: Let him cry out as much as he will; the more he mourns, the more we do acknowledge the iron rod upon his back. Therefore as many of the Theatines as should preserve even to the end, the truth kindled among them, they should see this joyful day with their eyes and should be partakers of the victory. Not that it should be necessary for them to be alive at that time, which arose about the year 1300, but because that is wont to be attributed to all which are of the same condition, that happens to any of them, to wit, to them who should be alive at the end of this period. For so the communion of saints requires that those few should be all.

And as the potter, etc., it is without any hope of restoration, even as the fragments of earthen pots, which are for no use. Let then the Roman Pope sweat and move every stone, that he may recover his former authority: he strives in vain, his fall is unrecoverable: he shall find no glue, whereby his earthen vessels may again be joined together. That in the end, as I have received from my father, signifies that this power shall not be obtained without blood, for Christ first suffered and so entered into glory. So Christians after some dangers and battles, yes overthrown in war, as we know to have fallen out in Frederick Saxon, Philip the Landgrave, and their armies, shall obtain this dominion over the Papists, as we shall show more fully in his place.

28 And I will give him the morning star: another reward no less agreeing to the times. This star is Christ, as we shall see later in 22 ch., where he says, “I am the root and generation of David, that bright morning star”; so called, partly because in this life he imparts to the saints himself a pledge and first fruits of true glory, lest long desire discourage them in their minds. Partly he takes this name in respect of the diverse administration of things. When he shines fully, he is both the morning star, the Day, and the Sun; but when he gives a lesser light, yet still gives hope of the perfect day that follows in time, he is the morning star, the precursor of the Sun. And we must know (which will become clearer in the following exposition) that a bright light of truth, of all godliness and religion, will shine upon the earth when our Jewish brethren are converted to Christ. Seeing therefore that then will be the full day, that renewed Church which goes next before, is the day star, which in the morning, seen near the horizon, shows that the fountain and spring of light will soon appear. And this Church is the reformed one, which succeeds Thyatiren, taking its beginning after the year 1520. The full restoration of the Jews follows at its heels, as the Sun the morning star. What is presented here is only barely alluded to, but may be sufficient to illustrate this point; the subsequent treatise will add proofs. Therefore, in this place the promised morning star is that sweet communion of Christ, which one shall enjoy in the reformed Churches, in which he shall be enrolled as a citizen, and which communication will be followed by the full happiness of the saints, as great as it can be on earth, shortly thereafter.

29 Let him that has an ear. The usual epilogue, but to be observed by reason of his diverse placement. For what end in the three first epistles is the reward set after the conclusion? In the four last this epiphoneme holds always the last place. First, the spirit teaches that there is a certain difference between the three first and four last, which we have observed, distinguishing all the seven into the three first churches growing worse, and the four last waxing stronger after sickness and feeling themselves somewhat better. Secondly, there may be another reason, which I gather from the event, that the rewards in the three first, as to eat the fruit of the tree of life in Paradise, not to be hurt by the second death, to eat the hidden manna and so on, were not paid suddenly and in one moment, but pertained to a time far off and delayed.

Whence do we follow the epiphonemes, as though after the admonition they should take time to deliberate: but in the four last they go before the epiphoneme, as if the admonition once given there should be no place left to take counsel, but the thing forthwith should obtain an issue, beyond all expectation, together with the deeds and sayings. And so we know it came to pass in the reformation begun by Luther, which we have shown to be a reward in respect to the antitype of the Thyatiren state. Who would have believed that from such small beginnings that thing could have gone so far at length? Luther indeed thought nothing less than any alteration or deviation from Rome, or who could have expected in such a small space such a great change of things? But now was the time when there should be power over the nations; and therefore the matter once begun proceeded of its own accord, an alteration of those things being made in a moment, whereat the world then not without cause was astonished, and at this the enemies do at this day behold with such heavy eyes. It seems that there shall be the same swiftness of the following rewards, which a man shall see given before he hears that they were to be given: and therefore in place they go before the admonition, which also no less they shall go before in time. You therefore, O Papists, you again I speak to, if peradventure the Spirit has given any of you ears, that you may hear: attend diligently those things which have been spoken. See what a one is your Rome which you embrace with so great reverence, and where you ran last year to celebrate your wicked jubilees: she is not a holy virgin, as you are persuaded falsely, but a most impudent Jezebel, a most cruel murderess of the saints, from whom we ought rather to flee into any wilderness with Elijah than to run to her by sea, by land, leaving at home the most chaste spouse of Christ. Behold also that this sorceress had lain sick now many years ago: (can you otherwise deny it?) which calls the Turk to come upon the Christian world, exiles our brethren out of their places of abode, turns them out from their goods, spoils them of their children and wives, and constrains them to be carried away into most cruel servitude, and heaps many calamities upon us all, which are far from that burning hatred. And not only these things at this present, but which shall bring finally a horrible death upon you your children. Can it be doubtful to anyone who shall weigh diligently these things with himself; but that we ought to flee very soon and very far from this plague and mischief? The Spirit give you ears to hear; I will speak no more; to them of whom the truth is esteemed, a bare signification of the will of God shall be sufficient: let him be filthy still, who shall despise this.

I will turn myself to the unfolding of those things that remain.

CHAPTER 3. (BOOK 3)
1 AND to the Angel of the Church which is at Sardis write: These things say who has the seven Spirits of God, and the seven stars: I know your works, to wit, that you are said to live, but you are dead.
2 Be vigilant & strengthen the things that remain, ready to die: for I have not found your works perfect before God.
3 Remember therefore how you have received and heard; and observe, & repent. That if you do not watch, I will come against you as a thief, neither will you know what hour I will come against you.
4 Notwithstanding you have a few names even in Sardis, which have not defiled their garments, and therefore they shall walk with me in white: for they are worthy.
5 He who overcomes shall be clothed with white garments, neither will I ever put his name out of the book of life, but will profess his name before my father and before his Angels.
6 Let him who has an ear hear what the Spirit says to the Churches.
7 And to the Angel of the Church of Philadelphia write: These things say he who is holy and true, who has the key of David; who opens and no one shuts, shuts and no one opens.
8 I know your works: behold I have set before you an open door, neither is any man able to shut it: because you have a little strength, and have kept my word, and have not denied my name.
9 Behold I will give those who are the Synagogue of Satan, that is, of those who say they are Jews and are not: Behold, I say, I will cause them to come and worship at your feet and to know that I have loved you.
10 Because you have kept the word of my patience, I also will keep you from the time of temptation, which shall come upon the whole world, to try the inhabitants of the earth.
11 Behold I come quickly, hold what you have: that no man may take your crown.
12 He who overcomes, I will make him a pillar in the Temple of my God, neither shall he go forth any more: and I will write upon him the name of my God, and the name of the city of my God, that is, of the new Jerusalem, which comes down from heaven from my God, and my new name.
13 Let him who has an ear hear what the Spirit says to the Churches.
14 And to the Angel of the Church of the Laodiceans write: These things say Amen, that faithful and true witness, the beginning of the work of God:
15 I know your works, to wit, that you are neither cold nor hot; I wish you were either cold or hot.
16 Therefore because you are lukewarm, neither cold nor hot, it shall come to pass that I will spew you out of my mouth.
17 For you say, ‘I am rich, and increased with goods, and have need of nothing’; and do not know that you are wretched, and miserable, and poor, and blind, and naked.
18 I counsel you to buy from me Gold tried in the fire, that you may be rich: and white garments, that you may be clothed, and that the shame of your nakedness may not appear; and that you anoint your eyes with eye salve that you may see.
19 As many I love I rebuke and chasten.
20 Be hot therefore and repent. Behold I stand at the door and knock, if any shall hear my voice and open the door, I will come into him and sup with him and he with me.
21 He who shall overcome, I will give him that he may sit with me in my throne, as I have overcome, and sit with my father in his throne.
22 Let him who has an ear hear what the Spirit says to the Churches.

The Analysis.
There are three Epistles in this chapter: one to the Sardenses, another to the Philadelphians, the last to the Laodiceans. Neither are they without cause included in one chapter, seeing they are of a somewhat diverse nature from the former. For the former were further distant from one another, so they had antipodes of a longer time; but these are both separated from one another with lesser distances, and also we shall find the Churches directly answering unto them, to be of a more conjoined time. The Epistle to the Sardenses after the inscription to the Angel describes the Sender from the seven Spirits, and seven stars: after it adds the Narration. Which reproves him, that he carries the name and some show of life, when in very deed he was dead, verse 1, but together also he teaches the remedy, which is double: the first consists in confirming the other things that are ready to die. For it should come to pass, that by the just judgment of God many should die, who so should punish the neglect of lawful and just amendment, verse 2. The second, that he should remember what things he had received, and should repent. Which admonition, lest he should negligently regard, he is sharpened by threatening of his unexpected coming, verse 3. After he praises some for their pure garments. Which praise contains the reward, both proper to them, and also common to all conquerors verse 5. Which is threefold, white clothing, a permanent name in the book of life, and his professing of him before his father and the Angels. All which are concluded with the usual Epiphoneme verse 6.

Scholions.
1 To the Angel of the Church which is at Sardis:* 1.1 Sardis is the second of the Churches rising again, going yet further in the South, and growing in a more ample light of truth.
The Antitype is the first reformed Church, begun by God by Martin Luther of Wittenberg, a town of Saxony on the River Elbe, in the year 1517, when that holy man opposed himself against the Roman Catholics selling for money the forgiveness of sins to the people.
The truth began to be revived under the Thyatiran state, but no reformation followed; This was first undertaken at the time which I have said.
For which cause we shall find no mention in these three Churches of this Chapter, either of Balaam or Jezebel.
For they were pure from the fault of this whore, whose fellowship they renounced utterly.
But yet notwithstanding seeing the same should not be done of all after the same manner, but a threefold difference would be found in them, in like manner they are shadowed out by three cities according to the beginning and condition of every one.
The first, after the impudency of Jezebel restrained, is Sardis.
And the first after the Roman impudency weakened, is the German Church of that time, which even now I have set down.
Only the indifferent and good readers are to be entreated that they do not think me to descend to this or that interpretation by any ill will, but in good faithfulness to follow that sense, which the printed steps of the Spirit going before, seem to me not darkly to point at.
I know how fearful a thing it is even to hurt the estimation of any brother with wrongful suspicions, how much more heinous a sin it should be to cast any blot rashly upon any whole Church?
And certainly as in all my life I desire to put far away all virulence of tongue, so especially I have thought always that I must take heed that I make not the name of God a cloak for my lust.
Let not then the office of an Interpreter be any fraud to me, speaking either here or in other places of things present otherwise peradventure than many either would or expect.
It is an impious and detestable thing, to play the hucksters with the word of God, in speaking rather according to the pleasure of men, then the truth of the thing itself.
Therefore all as well hatred as favor set aside, if we shall see that that which is uttered agrees with the truth, let us quake rather at the threatening of the most just God, then be angry with him, who to the end that we may not be oppressed unawares with the evils hanging over our heads, hath endeavored to his utmost power to reveal the hidden truth.
Which I hope I shall obtain easily of all the godly, so far shall it be from them, to reprehend mine industry: with which hope supported, I will proceed to my purpose through God’s help.

¶ These things says he that has those seven Spirits of God, and those seven stars: In the description of the sender of the Epistle, of those Spirits which are recalled, there was no mention in the vision of the first chapter. They are fetched from the common inscription of the Epistle in the first chapter, verse 4. They are seven for the abundance of all gifts, which that number usually signifies. Christ has in his own power, that being the keeper of the storehouse of heavenly grace, he bestows the Spirit on whom he shall think good; whereupon he says that he will send the Comforter from the Father (John 15:26), who should receive from Christ, and show unto us (John 16:14).

The stars are in the right hand, chap. 1:16. Likewise in the Ephesian Church, where we have heard declared the safety of the ministers, whom Christ carries in his hand, chap. 2:1. To what end then is this repeated again? Was there now any other honour spent wholly on the former? In no way, but only because of the convenience of matters, and not any vain novelty, is sought. Because Sardis should find the same safeguard of Christ in defending its pastors, which he had shown in Ephesus; not without reason does he use the same similarity, wherein there is such great connection of matters.

But of Sardis the history speaks not a word, which thing in its antithesis is most clear. For he that gives the Spirit plentifully, to whom and when he will, sheds out in those times so great plenty of all gifts, as nowhere else in these last times. Good learning had already been buried, being driven away for many ages by the rusticity of the Scholastics. At length, after the wonderful art of printing was discovered, many excellent wits were raised up to search out the truth. Among them were John Picus Mirandulanus, Angelus Politianus, Platina, Trapezuntius, Gaza, Hermolaus Barbarus, Marsilius Ficinus, Pyrbachius, Joannes de Monte Regio, Aldus Manutius, Rodolphus Agricola, Joannes Jovianus Pontanus, Philippus Beroaldus, Joannes Reuchlinus, and many other most learned men; whose chief labour was in setting forth the tongues, arts, and other human learning. But how great an entrance was made from here to uncover the mysteries of salvation, the conjoined times have taught.

For by then, after came Martin Luther, Philip Melanchthon, Erasmus of Rotterdam, Zwingli, Oecolampadius, Capito, Blarer, Bucer, Musculus, Calvin, and many other most learned men—so many lights of the Christian world—who, being helped by the studies of those before, brought forth again the truth, covered with long filth and uncleanness, dissipated the Roman darkness, and dispelled utterly like smoke hither and thither all the subtleties of the enemies. Does Christ not rightly take upon himself this banner of the seven Spirits, enriching this time with such a great abundance of gifts?

Neither was his power and grace less famous for conserving safety to the pastors. Who would not have thought that Luther, in so great hatred and envy of all men, for whom almost the whole world laid wait—even he under whose feet the emperors once were compelled to subject their necks—that Luther, I say, should have died a thousand deaths? But perhaps troubles being raised he did scarce endure; yet by almost thirty years he abided in the battle safe, even from private assaults, with which the Pope is wont to make away those men whom he cannot conquer with open war and force: and at length, lying sick in his bed and giving up his soul to him that gave it, he slept quietly in Christ.

What should I speak of Melanchthon, Peter Martyr, John Calvin, and the rest of the valiant heralds? Bucer, buried a few years earlier, at last turned to dust, was dug out of his grave, or rather another buried there recently, so that they might show their cruelty even in the burning of his ashes, whom they could not, nor dared to, hurt while he lived. Who then has not seen the stars in the right hand of Christ, so wonderfully defending his servants against all adversaries? And should not the fresh memory of these things give constancy and courage to all, so that, relying on the same protection, they may boldly go to the defense of the truth, each according to his calling? There is indeed not the same explicit promise as in other times, yet there is always the same crown for those who fight lawfully.

¶ I know thy works, that thou art said to live, but art dead: A reprimension for their counterfeit life, of which the angel bears a shew, being void of truth: from whence Sardis may be called Hypocritical. The force of which notation is manifest from the name itself. For Sardis as Sardinian laughter, such rather in shew, then in very truth; so called of the city Sardis, even as the Sardonian laughter, of the Island Sardonia, as Erasmus notes from Plutarch.

For that kind of herb ranunculus in English trowfoot, by which the mind is taken away, may grow as well in Lydia as in the Island.

This Church was counted alive but was dead: like unto this laughing, which feigns joyfulness, in the mean time full of deadly sorrow. And from hence it is evident how Sardis is opposed to Smyrna; This found all outward things most troublesome, so as she was almost held of all for dead; yet in the mean time live a true life, and was most acceptable to God: That abroad in the judgement of men liveth and flourishes excellently, yet within, death reigns, true godlines being banished: From whence is made the second pair of contraries, as was observed in the common analysis of the seven Epistles.

But in what thing consisted this fawning, as far as concerns the city Sardis, it is not clear to us from the history: there flourished in the same place not very long after, the famous Melito, celebrated by Eusebius in his 4th book, chap. 26. But hence it appears that the matter was brought to that case when John wrote, that although the angel seemed to himself, and peradventure to some others, excellently well furnished with all things unto salvation; yet that he wanted many things necessary, and abounded in the contrary.

We know that those who are alive outwardly may be dead either in ignorance of doctrine and corruption, or through careless of Godly duties: as Christ calls them dead, which were void of faith and knowledge of salvation, John 5:25. And the Apostle calls the wanton widow dead when she is alive, however she had given her name to Christ, 1 Tim. 5:6. In which respect also works are called dead, Hebrews 6:2, as declaring that they are indeed dead that give themselves up to the study & love of them.

It may be that partly through neglect of godlines, partly by corruption of doctrine the angel of Sardis fell into this dead life. If the doctrine had been quite extinguished, which in deed is the soul of the Church, she could not have obtained even the name of any life.

We have said that the Antitype, because of the following order of things, was the first reformed Church, springing up in Saxony, when Luther began to teach. For the Thyatira Church have some blame for suffering the Roman Iezabell. This first, as Iehu, laboured that the painted & shameless whore should be cast out of the window, so as she did sprinkle the earth with her brain.

From whence it comes to pass, that she is not rebuked so much as in one word in respect of this. This Church then has the name that she is alive, for the truth restored, which in wonderful manner she has manifested; and also for the excellent courage, whereby she weakened and trod under foot the Romish tyranny, shaking of the same not only from her own neck, but also giving the same to be derided of the whole world: yet she is dead, having some errors and corruptions of no small importance, chiefly that consubstantiation of the body of Christ in the sacrament of the supper, which many other absurdities followed, which does spread like leprosy, and take away the life of the members living by themselves.

Notwithstanding these things are not to be understood of every man, but of the whole policy and form of the Church, which is apparent to the world: the image and proportion whereof, the Spirit portrays to us. Which also is to be observed in the rest.

2 Awake and strengthen the things that remain ready to die: The first remedy is diligence in confirming the rest; who, if it were not with all speed looked at, would rush into the destruction of death. By which it is taught that if the teachers would bestow faithful and diligent pains, in cleansing the whole doctrine and doctrines, they should take away from many the occasion of falling; but if they shall carry themselves over negligently in this matter, there would be a lamentable ruin of many. In the antitype the thing is so clear, that any man may be waylaid with tears, rather than to prosecute it in words. For how many excellent men hath that monster of ubiquity cast headlong into death? The seeds of which Luther sowed in the years 1526 and 1528 in a disputation against Zuinglius and Oecolampadius. But they ought to have been pulled out again from his books, at least after the controversy was brought to sleep, lest lurking as it were in the furrows, they should break forth at length into deadly hemlock. But Luther himself was careless thereof, providing after the manner of men rather for his own estimation then, as was meet, for the safety of the brethren. Moreover I find lack of your faithfulness and diligence, o holy Philip: because thou hast not thrust through so foul an error according to his due. Perhaps you thought it was to be handled more gently by you, partly in favour of thy friend, partly because you supposed it might be abolished by silence more easily than by sharp inveigling of words. But the errors which are not refuted seem to be allowed, and their estimation grows so much the more as they are dealt with more gently: for they are gangrenes, which gentle remedies do not heal but make worse. While therefore neither of you watches nor does his duty, many die: how many I pray, and how great men? An huge number in deed of all degrees: of which the principal as standard-bearers were Iohannes Brentius, Iacobus Andreas, Selnecerus, Kirchnerus, Chemnitius, and others of that sort, who have increased this monster of ubiquity, of itself horrible, with so many and notable errors, that there hath been scarce at my time any other more foul and deadly. Lamentable in deed is the fall of the famous men, whose labour was once courageous and no less profitable against the common enemies. And what a crown had they received, if they had continued in the same warfare, and had not as cruel elephants turned back the enemies, wasted their own friends. But my office is of an interpreter and not of a quereller: and therefore I leave these things. This death invaded not only some particular men, but also many whole cities and provinces, as may appear by the book of Concord published in the year 1580, which is not of so great force to establish the error with the consent of so many, as to testify this miserable calamity of the brethren. And to this error touching the supper of the Lord, and person of Christ, were many other also added, to wit of original sin, of free will, of justification, of good works, of the law and gospel, of indifferent things, and of predestination. Therefore death assaults with a manifold dart: how great must the slaughter be, seeing she cast to ground even with one, great troops of men?

¶ For I have not found your works perfect; the reason why so many fell into death. The Church of Sardis, as far as it seems, admitted not the sincere truth of God, but retained some ethnic superstition. The Church of Germany did indeed cast away many popish errors, yet in the sacrament of the supper, she stuck still as it were in the clay of bodily presence, not as Rome, dreaming of a changed substance of bread and wine into a true and real flesh and blood, but no less contrary to and disagreeing with the truth, conjoining the true flesh and blood together with the outward signs, affirming that he is present here on earth. This leaven Luther never cast out, but contended fiercely with Zuinglius & Oecolampadius, for to defend & retain the same. Neither would God, which afflicted so grievously the Corinthians for the profanation of this sacred mystery, so many were weak and sick, and many slept, 1 Cor. 11:30. have gone away unpunished the neglect of amending in this point. Of which punishment to come some proof was made, when Luther was constrained for the defense of an unjust cause, to fly for succor to Vbiquity and to confirm many other things touching the manhood of Christ, which are contrary to the truth. But for the heat of contention, he could not so well consider and mind, that from those beginnings and flourishes, he should understand God to be angry. How did he not beware of that error which did draw with it so great a multitude of wicked opinions? Why feared he not, what might have happened to others, having tried in himself, into what case he himself was brought in disputing? But his eyes were held, that he could not foresee for the time to come, and turn away this so grievous punishment from his people. Therefore their works were not perfect, because a full reformation was not used, but only one error changed into another not less grievous.

And God is wont often times to punish sin with sin.

3 Remember therefore etc. The second remedy is, to remember and repent; Theod. Beza translated thus: remember what thou hast received. And so indeed some time the word pos seemeth to be taken. For that of Mark take heed what thou hear, chap. 4.24. Luke hath it thus: take heed how you hear, chap. 8.18. But when he said even now, that their works were not full before God, he seemeth not so much to exhort, that they would retain those things which they had received (for so they should have continued in their former errors) as that they should remember the manner of receiving: So as pos in this place ought to remain in his own proper signification, denoting rather the quality, then the substance of the thing. He warns therefore the Sardenses, that they go back to the first institution, and amend things fallen into decay, after the rule of that alone: Even as also the German Church, that they mind what Luther propounded to himself at the beginning, and make their reformation according to that rule. But he regarded no other thing at first, then that all human inventions driven away, only the divine truth revealed in the scriptures inspired of God might prevail. For so in the preface of his assertion of the articles condemned by the Bull of Pope Leo X. First, he says, I will that they bear me witness, that I will not be compelled with the authority of any at all, how holy a fathersoever, unless as far as he shall be approved by the judgement of divine scripture: Again, let the first principles then of Christians be none other but the word of God: but all men’s conclusions be fetched from hence, and again reduced thither and tried thereby; Those first of all ought to be known to everyone, and not sought out by men, but men to be judged by them; Whereupon also he reiterates that Augustine’s third book of the Trinity is not bound to my Epistles as to the Canonical Scriptures, etc. Therefore we may not cling to Luther’s books, as the Vbiquitaries do, and those who corrupt the Sacrament by the late devised consubstantiation, but as he thought he must be wise only out of the scriptures, all his writings are to be brought back to these holy balances. Why do we give greater authority to his books, than to the books of others, or would he himself have to be given to his own? A matter indeed of great moment, and in which alone consists the turning away of the eminent evil. Unless men turn their eyes to these things, and have their ears bent to hear their voice, and also those things performed which they shall command, another scourge remains for Germany more bitter than that, which even hitherto has afflicted her not lightly. What godly man takes not great grief minding the destruction of so many brethren by a pernicious error, so long contentions of minds, so sharp battles both of words and weapons? But he must need be more vexed when he considers with himself that there is not yet an end to these evils, but some greater thing to hang over their heads, unless they repent in time. I could not but warn the brethren of the danger, lest I should hear with my great grief that they are afflicted and full of calamity, whom I desire in Christ Jesus to flourish. And I hope that however my judgement shall be troublesome, yet my good will shall not be ungrateful.

¶ If you do not watch, I will come, etc. The danger that He threatens is His coming like a thief, at an unexpected time. He does not expressly say what kind of evil will come, although part of it may be inferred from the simile, which is often used in Scripture to signify the invasion of the enemy. But seeing the following words have respect hitherto, you will not know at what hour I will come against you, perhaps He means something else, namely a certain force and violence, such as thieves use in robbing houses: who not only spoil the owners of their goods but also commit adultery with their wives, deflower virgins, and force confessions of where money is hidden; having obtained it, so that their wickedness may not be betrayed, they kill all without distinction of sex or age. Therefore, Christ appears here to threaten the same outrageous ferocity of some cruel enemy.

Of whose coming we may not define by the judgment of the flesh, seeing it shall not be known in what hour He shall come. Neither must we labor much to search out who this enemy should be. The Spirit, who has determined that his coming shall be sudden, would not have him known by name. It may be that it is the Turk, to whom the reins may be loosened awhile, until they be looked at that are to be punished. But whether it shall be he or some other, we may not sleep securely and neglect reformation, because we see no danger at hand; but we must think how it may come upon us in a moment. And it is to be feared that this which is threatened shall no more be avoided than that of removing the candlestick from the Ephesian Church (chap. 2.5). These things depend on the condition of repentance, to which the ears of men are deaf, even the greatest part.

4 Yet you have a few persons; in Greek it is a few names, that is, a few men, as Acts 1:15 and after in this book chapter 11:13. In these words he comes to the other part of the narrative, which pertains to commendation. Which always, at other times, tends to take the first place. But this new disposition and setting in order is not done rashly, teaching that in the latter times shall be some who refusing errors should embrace the truth. As we know, it was done when the Book of Concord began from this occasion, and so many visitations were undertaken, that the Calvinists, as they speak, might be rooted out utterly. For such men, followers of true godlines and judgement, were conversant in the deepest parts of this Sardinian state. Besides many free cities such as Strasbourg, Heidelberg, Marburg, Newstadt, Bremen, the people of Anhalt, etc., who opposed themselves against the forgeries of others. In every one of those places famous lights now and then did shine, which drove far away that darkness, gave a joyful day to their flocks.

¶ Which have not defiled their garments: The garment is Christ himself, the common clothing of all the faithful. Of which, in the parable, “Friend, how have you come hither,” not having on a wedding garment, Matt. 22:12. And Paul more plainly, “For all of you who have been baptized into Christ, you have put on Christ,” Gal. 3:27. But it has a diverse signification according to the diverse respects of things into which it is referred. In respect of God, it belongs to justification; in respect of other people, to sanctification and profession; in respect of ourselves, to honor, glory, triumph, joy, etc. Therefore these Sardinians kept their profession of Christ sincere and entire, free from the filth and pollution of those monstrous opinions. Although they too, by repentance, awoke from those errors, may be said to keep their garments also pure. For those who are in Christ are not judged by their former filth, but by their present apparel, with which all their former uncleanness is covered.

¶ And therefore they shall walk with me in white, to wit, garments. These are the same garments with the former, but a little differing in respect; for those were of profession, whereby the valiant soldiers of Christ did appear to others: these are of glory, triumph, and joy, which they shall enjoy both in themselves from the feeling of God’s love shed abroad in their hearts, and also which they should receive from the praising of others, who shall praise God in their name, who has bestowed on them fortitude & victory. A white and pure gown in a solemn mirth is commendable, both among the Gentiles and also the people of God. From whence the wise man alluding to this manner, Let, says he, thy garments be white always, Eccl. 9:8. But especially I think that of Mark is to be regarded, where some step of this celestial glory appeared in the shining garment, so white as snow, such as no fuller can make on earth, Ch. 9:3. At which sight Peter, being overwhelmed with unmeasurable joy, thought this one thing, which way he might have been able to enjoy it always. So this shall be a most ample reward for the saints in which they shall so heartily delight, that they shall desire no greater thing in this life.

And if any should ask the brethren themselves, whose these garments are, I doubt not but they would answer, that this joy is of more value, which they obtain by Christ in retaining his truth, than that they would change it with all the delight of this life. Certainly great is their glory among all the godly, which we pray with all our hearts to be perpetual to them.

¶ For they are worthy. The Papists are glad in their own behalf for this word, as an excellent patron of their merit of condign worthiness: but let them remember that this merit is attributed to the garment, not to the body, that is to the imputation of the righteousness of Christ, wherewith we are clothed as with a garment, not to our inherent holiness; For not to defile the garment cannot be more esteemed than the garment itself. And seeing there be sundry significances of the garments, as we have shown, the worthiness arises not either from the profession of good works, whereby the saints are seen by others, nor from the joy of the Spirit, which we ourselves feel within us, but from this alone: that the Father counts us righteous being clothed with His Son. He, therefore, is worthy to be clothed, though not in every use of garments, but only in that peculiar respect whereby we are presented blameless in the presence of God: even as a man sees, although not the whole man, but only that part to which the faculty belongs.

5 He that shall overcome &c. Some copies and the common translation read thus: He that shall overcome shall be so clothed. But the rendition of a similitude is unusual, where there is no question: unless peradventure they are referred to the former verse, as though he should say, as those who at all have not assented to errors, shall walk with me arrayed in white apparel, so that those who after some striving shall depart from the same, shall be clothed in white. As though the first reward were pertaining to those who fell not, this to those who repented and forsook their errors, with which they were possessed before time. Of this sort were many in Germany before the book of Concord was published, when in most universities the chief teachers understood the true doctrine of the supper of the Lord, and the opinions of ubiquity and corporal presence in the supper, everywhere were contemned, as witnesseth Georg. Sohnius in his exposition of the August Confessions, which appears more clearly from the Synod of Desdrense, in the year above 1571, where it was ordained by the common consent both of all the superintendents of the Duchy of Saxony, and also of the doctors of the universities of Leipzig and Wittenberg; that the ubiquity of the body of Christ was a horrible profanation of all the articles of the Creed, and a renewal of all heresies, Gallobel, in the year 1592. And since that time a fierce light breaking forth every day, many were roused up from their drowsiness, and opened their eyes to the truth. Whom also even as well as the other, he adorns with white garments, who gave a penny to those who were hired at the eleventh hour, Mat. 20.9. Such then is the first reward, though yet does remain.

¶ And I will never put his name out of the book of life; the second reward applied to the times. For because very many in these times should fall from the truth, and many cities, peoples, provinces, regions, should consent to error (as at this time it is evident how far and wide the contagion spread abroad, flying also over the sea and infecting those Northern regions Gothia and Suecia) by which their approving of error they should blot their names out of the register of the saints, and should cut off from themselves the hope of life, unless they should repent, lest I say, the falling away of so many should trouble the saints; he bids his conquerors to have good courage. Christ Himself would set them free from falling, however they might see infinite numbers rushing down violently on their right and left hand. For it is He alone, who first calleth us back from error, then sanctifies and confirms us in the truth, lest at any time we should revolt from it. Therefore, however this reward be full of comfort, yet it teaches that the time should be lamentable through the fall of many. For to betray and forsake the truth is not a light matter, as many suppose, who easily are carried away with every wind of doctrine, but it is an argument of a man of no reckoning with God. But how, wilt thou say, can they be blotted out, which once were written in the book of life? Especially seeing that this book is the book of the Lamb, as in chapter 13.8, that is, wherein those that are written, the Lamb acknowledges them for His, and counts them heirs of eternal life: neither is there any of those that are given to Christ, that can ever perish, John 6.37, 6.39, and 17.12. I answer that these things are spoken in respect of us. For there is a twofold book of life, one, as I may say, of vocation, another of election. Into the first are put all, who by the preaching of the Gospel are taken into the fellowship of the Church, who rightly do seem unto us to be partakers of life, and endowed with the hope of eternal salvation. For the scriptures are wont to speak so generally, giving thanks to the Father, who has made us meet to be partakers of the inheritance of the saints in light: who has delivered us from the power of darkness, and translated us into the kingdom of His dear Son, in whom we have redemption by His blood, the forgiveness of sins, etc. So the Apostle speaks of the multitude of the Colossians without difference, chapter 1.12. And after the same manner everywhere in other places. Yet men may be put out of this book. For many are called, but few chosen, Matthew 22.14. And it is declared later in the 7th chapter by an example, Dan and Ephraim being passed over in the rehearsing of the tribes, as soldiers put out of wages, and cast out of the register. For God of old, as in a certain visible shadow of this book, commanded the genealogies of each tribe among the people of Israel to be kept diligently. Whereto also pertained that of raising up seed to the dead, that his name should not be put out from his people: Deuteronomy 25.6. In which respect also the Psalmist wishes to certain reprobates, who held a place in the Church, like true citizens, that God at length would separate them from the congregation of the Saints and manifest them to be mere hypocrites, Psalm 69.29. Wherefore all are put out of this book of life, who forsake the fellowship of the holy Church, either through error and heresy, or wickedness, or other cause whatsoever: not that for this cause they are blotted out of the book of Election, but because by this way they make manifest that they were never written in this book; as John says, they went out from us, but they were not of us, 1 John 2.19. But the other book, to wit, of Election is never spotted with any blots, but the names once written remain constantly without being erased. Although these books are not so open and evident, that they can be read by all men without difference: but it is declared to every one separately by the Spirit that is found in this register, in what estimation and account he is.

¶ But I will confess his name: The third reward is of confessing their name. Which shows not only the falling away of many, but also that others shall be compelled by force: So as there is great need of the power of the Spirit, lest any weakened by the injuries and threats of adversaries, do forsake the truth. For the confession of their name before his father is for the comfort of confessing Christ and his truth boldly and without fear. So sending his Apostles to preach, furnishes and instructs them against the fear of affliction, Matt. 10.32. And who knows not to what inhumanity and cruelty proceeded the hatred of those who call themselves Lutherans, against the professors of the truth? In the year 1580 was imposed upon the Ministers of the Churches, and Schools the book of Concord, avouching the execrable error of Vbiquity. A subscription was commanded in the name of the Princes, the refusers were proclaimed Sacramentaries, or put out of their places. In the year 1591 Christian Duke of Saxony being dead, Paul Kreilius Chaunceler, suspected of Calvinism as they speak, was cast into prison: Vrbanus Pierius, Professor of Wittenberg, was led captive into prison: Gundermannus of Leipzig, committed prisoner. In the following year was appointed a new visitation, they went through all Saxony: those who would not subscribe to the articles were removed from their offices.

What should I rehearse the brawl of Leipzig the year following, when all the university men on every side assembled together to break open violently the houses of the Calvinists?
Or the savage cruelty of the Dressens against the dead body of Jac. Lassius, to which they denied a grave among the wicked, because being alive he was a lover of the purer truth?
I recite these few against my will, & I would be ashamed to mention them, but that the brethren were not ashamed to commit them.
But how much better is it for you to hear these things of your friends, then of your enemies?
These as much as they can do exaggerate with words your evil acts, unto your perpetual shame & of all religion: I do only show the congruence of the Prophecy, that seeing in what account you are with God, you may think earnestly of reforming the errors & making peace with the brethren.
God give you to see that way, whereby consenting to one truth, you may turn away the judgment from your heads, which otherwise will overtake you.
In the mean time if I shall prevail nothing with you (which estimation I pray may be far from you) yet I shall be glad to admonish the brethren, that they be of good courage, who do endure troubles and calamities among you.
Christ will not be ashamed of them before his Father, if they shall abide constantly in their profession.
Fear not therefore the stately look and countenance of men, but being grounded upon this hope, that which you have worshipped in darkness, profess now openly & in the eyes of all.

6 Let him that has an ear hear; Yet therefore brethren of Saxony, for Jesus Christ’s sake give ear and hearken, what action the Spirit charges you with. Your praise is great in respect of your first combat, and breaking off the yoke of Roman tyranny, yet you who in this were the first of all. But the Canaanites left in your land are come to be thorns in your sides and eyes. Those few errors neglected at first, by the just judgement of God, have brought forth new errors: by the contagion, where true godliness is driven away, and together with it true life is lost, there is left unto you a church defiled with horrible death. Neither is this the end of evils, but some new, great and sudden calamity shall come upon you unless you obey forthwith the Spirit, giving you warning. Therefore let that unhappy obstinacy depart and be packed away, and take those counsels which may promote the truth, recall again the banished life, and may procure the salvation and safety of every one of you. And do not only give ear, but let all hearken and learn from your evil, how great a danger it is to cherish the least error in the matter of religion.

Analysis.
So is the Epistle to the Sardians, this to the Philadelphians is inscribed likewise to the angel: He who sends is notable for holiness, truth and the key of David, which he carries not idle, but with the same opens and shuts, the supreme power being in himself, verse 7. The narration recounts first the good things, both present, of an open door, which is illustrated by his cause, a little strength and the constant observing of his word, verse 8, and also to come, both of subduing their enemies, verse 9, and also of ministering help in the common temptation; of which a reason is rendered, from their patience in the profession of the Gospel, verse 10. After he provokes them unto a care of preserving that which is good, because his coming is at hand, and there may be danger of their crown to be taken away, verse 11. Then there is a great reward, when he shall be made a pillar, and shall have written upon it the name both of God and of the new Jerusalem, and the new name of a son, verse 12. To all which is added in the end the common conclusion.

Scholions.
7 And to the Angel of the Church of Philadelphia; We have shown at the first chapter ver. 11 that Philadelphia is situated in a dangerous place, and therefore not so frequent of citizens, who did dwell scatteringly in the fields, fearing the often quaking of the city.
But she carries a sweet name, and which alone contains within it all virtues. Neither did the Apostle Peter find anything, when he would exhort to all godliness, which might commend more fitly the same unto us than brotherly unfeigned love, 1 Pet. 1.22. How well this name does fit this Church, which is reproved for no sin openly!
But as it was truly godly because of brotherly love, so is she lowly and not famous, both through a continual fear of danger, and also solitariness of the citizens, who dwelt here and there, and in waste places, where they could get safe dwelling.
Wherein she is altogether contrary to Pergamum, a towered and proud city, as before Sardis to Smyrna, and Thyatira to Ephesus.
And so there is made 3. pair of contraries. It lies from Sardis toward the South, having an increase of greater light, as becomes a reformed Church. She is set in the second place after Sardis (for this is the first after Iesabel overcome) whereby it is shown that her antitype is the second reformed Church, which should arise after the German, and this is the Church of the Helvetians, Suevia, Geneva, France, Holland Scotland. I join all these into one, because they live almost after one and the same kind of laws and ordinances, as touching the things that are of any moment.
Neither does the distance of place break that society which the conjunction of minds and will does couple. Yea this dispersion does agree chiefly to the Philadelphians, whom we have shown to dwell thicker and more frequent in the fields than in the city.
Whereby it comes to pass that this thinness of the citizens takes up much place, though the citizens are not so many. We shall find that this Church which I speak of arose a little while after the German; when Vlricus Zvinglius began to teach at Tigur in Helvetia, in the year 1519, and the reformation was begun the fourth year after, to wit, in the year 1523, at which time no Papist durst enter into combat against Zvinglius, who deferred the judgement of all controversies to the arbitration of the sacred scriptures. They of Constance, Basil, Strasbourg, Geneva and others, followed their steps. Where it is to be observed that the former antitypes were distinguished by longer intervals: these three last as they have types less distant one from another by space of place, so they are joined one with another with a nearer conjunction of times, neither are they divided so much by ages and limits of years, as by laws and customs. For after the first receiving, which happened to some later than to others: we shall see that they did all flourish together.

¶ These things say that holy one, that true one, who has, etc. A description of him who sent the Epistle: whose two first properties are taken from the nature of the sun of God, which yet are not rehearsed expressly in the vision of the first chapter: They do greatly help to declare the administration of this Church. Touching the city Philadelphia itself, we find no other thing, but that in the age following, there abodes in that place a famous congregation of the faithful, over which Demas had the charge, as is gathered from the Epistles of Ignatius. In the Antitype, a divine power specially shines forth sanctifying the Church, by kindling the desire of godliness, and in making it in Christ Jesus fit and cheerful to every good work. Let my words be without envy, the true doctrine sounds nowhere purer, the worship less corrupted, more flourishes the faithful diligence of the Pastors, is performed more willing obedience of the people, nor greater reverence for all religion among all degrees. But this holiness seems chiefly to respect manners. In which thing is not to be passed over that famous testimony of John Bodin, speaking of them of Geneva; Of whom that thing, says he, is praise worthy, if anything anywhere in the earth, and which makes a common wealth to flourish, if not in riches and greatness of Empire, yet certainly in virtues and godliness, namely that censure of the Pope, then which nothing greater and more divine could be devised to bridle men’s lusts, and to repress those vices, which by no means could be amended by any humane laws and judgments. How be it that this restraint is directed after the rules of Christ, first privately and friendly, after somewhat more sharply, then if you do not obey, there follows a heavy, grave and effectual prohibition from the holy things; after the interdiction, is the punishment of the Magistrate. And so it comes to pass, that those things which are punished nowhere by the laws, are there restrained without any force and stir or great ado. Therefore no whoredoms, no drunkennesses, no dancings, no beggars, no idle persons are found in that city, Those are his words in Method of History chap. 6. Worthily is the sanctifier of the Church to be prayed, who has wrought, that they should will and effect these things according to his free good will. There is the same care and fruit also of the rest, according to the measure, which Christ vouchsafes to every congregation of them. Neither is his truth less excellent, both in as much as he is a Prophet in teaching, and also a Surety in promising. We shall see this double truth in the following Church to be distinguished by their proper words; both which the Greek word true seems to contain, when it is put absolutely and by itself. And as touching truth of doctrine, where is it more pure and more sincere in the whole earth? The whole Papacy has here his throat cut. The Anabaptists, Antitrinitarians, Arians, and such like monsters raised again from hell, partly in Germany, partly in Transylvania, have found nowhere a fiercer enemy: What also has it not assayed, that she might pull away from the German Churches their errors? Neither does she keep only the doctrine of salvation uncorrupt, but also she both delivers and teaches in writings and exercises in practice a sincere manner of administering, whereby salvation is bestowed. Certainly the whole will of God is communicated with his saints, so as Christ takes to himself not undeservedly this praise of true in governing this Church: He also performs plenteously that which he promised, that he would keep safe and sound those that seek him with an upright heart. What have not endeavored the French man, the Spaniard, the Savoyan, the Pope, to root out them from Geneva, a small people, and surrounded on every side with enemies, and shut up from all aid of friends? Nevertheless it flourishes yet still thanks be to God, and shall flourish hereafter, while all her adversaries burst with envy: as long as she shall continue in this holy order. The French Church has been preserved hitherto, no other wise then the three children in the furnace. Who would have believed that the Low Countries had been able to resist and withstand the raging Philip, the cruel Duke d’Alve, and so many bloody tyrants? But true is he, who has promised this honour to his saints, that they should bind the Kings with chains, and their nobles with fetters of iron, Psalm 149:8-9. And that I may not speak of each one, they can be safe only by thy protection, O Most High God, who art constant in all thy promises, whom both enemies almost infinite do persecute with deadly hatred, and also to whom many of their friends through envy wish not very well.

¶ Who hath the key of David: The third property pertains also to the same administration. Christ opens and shuts, to whom he has thought it good, the entrance into the kingdom of Heaven, by his regal power. Which faculty in indeed he bestows upon all his who declares and preaches the word purely and sincerely, but which is principally to be seen in that part of government by which obstinate sinners who will not yield to admonitions are delivered to Satan by the ecclesiastical censure, and are cast out of the Church, which is the kingdom of Heaven: according to that, whatever ye shall bind on earth shall be bound in heaven, and whatever ye shall loose on earth shall be loosed in heaven: For where two or three are gathered together in my name, there am I in the midst of them: Mat. 18.18.20. By these therefore is shown that the power of opening and shutting, of binding and loosing is very effective in these congregations, and moreover also in the whole administration of the censures. And what godly man does not thank God from his heart, and does not exalt with worthy praises the holy pains of this Church, which restored discipline that had fallen into decay, and brought it back to the rule of truth and the use of the primitive Church?

But it is to be observed that this key was said before to be the key of Death and Hell, in the first Chapter 18th verse, by one part denoting the whole force of them. Therefore that key is to be feared, which locks up the gate upon the wicked being thrust into Hell, however they despise it with security: And yet notwithstanding it is less pleasant to them that fear God, because it unlocks to them the doors by which they may enter into life. But why is it called of David, seeing it is of Aaron rather, whose office was to keep away the leprous and uncleans from the holy things, and to shut the Temple against them? Certainly the Priest only could pronounce men uncleans: he was not wont by an ordinary & proper power to use force to compel the disobedient. Christ both King and Priest is very mighty in both faculties and powers, and joins together both in this Church: who not only raises up Pastors, that they should denounce men uncleans, but also together adjoins the civil Magistrate, that he should give his ready and diligent labour to the Pastors in this. So before Bod. the punishment of the Magistrate follows the debarring from holy things. Therefore both swords are drawn in this Church but separately by those to whom the one & the other belong. And indeed this society is most sweet, seeing all the industry of civil Magistrate ought to have respect there, that we may live with all godliness & honesty, 1 Tim. 2:2.

The words seem to be taken out of Isaiah chapter 22, verse 22: “I will lay, saith he, the key of the house of David upon his shoulder; when he openeth, no man shall shut, and when he shutteth, no man shall open.” But in this place the word house seems to have been omitted purposely; for he says not “who has the key of the house of David,” but “who has the key of David.” There is a difference, because the former seems to refer to an inferior minister in the family of David, whereas the latter refers to a supreme governor of a whole kingdom. So the omission of one word creates a difference between the type and the truth, between Eliakim and Christ. See also Isaiah 9:6–7. The Complutensian Edition and the King James Bible read somewhat otherwise: “Who openeth, and no man shall shut; who shutteth not, and no man shall open.” Arethas has “except him who opens.”

8 I know your works: behold, I have set before you an open door. He enters into the narration, and first of a present good thing. And it is an open door, which sometimes signifies the faculty of preaching the Gospel, for which Paul earnestly desired of God on his behalf, that the door of utterance might be opened to him, Col. 4:3, and that speech might be given unto him in opening his mouth, Eph. 6:19. And worthily is it so called, seeing by the word a door is opened to us into heaven, which being taken away and removed, the door is shut and locked, so that no one can enter in, Luke 13:25. And not only the faculty of the ministers is the door, but also the readiness of the hearers, as, “For a great door and effectual is opened unto me, and there be many adversaries,” as though he should say, although there are many who do resist and strive against the truth, yet there are many whose desire is prompt and ready, 1 Cor. 16:9. And again, coming to Troas to preach the Gospel, “and a door being opened to me in the Lord.” This door is opened when the hearts are opened to receive the truth, as Lydia, whose heart the Lord opened, that she might attend to those things which were spoken of Paul, Acts 16:14. But although the name of door be attributed to those apart, yet most of all the door is then opened when all these things meet jointly together: the word, discipline, the care of the magistrate and of the people. Then there is free leave to pierce into the consciences of men, unto which an entrance is shut up where any of these shall be wanting. This then is that open door whereby this Church was famous, which indeed no strength of wit has opened, which consists either in the virtue of speaking, or in the sharpness of wit and prudence in understanding, but only that chief key‑bearer, who has given freely that which no man could have obtained by human strength. How ungodly therefore are they who do check by reproachful words that which Christ has conferred for an excellent benefit? They whet their tongues against heaven, yea, against God himself; but they shall not escape unpunished, let them clatter as much as they will.

¶ Neither can anyone shut it; the endeavor of the adversaries has not been lacking; some have labored to bar these doors by slandering, reproaching, inveighing, with all manner of contempt; others by force and weapons, as it were by a rushing down violently to shoot this gate, but he has performed his promise, who has confirmed that none shall prevail. The enemies have lost their labor and have gained nothing but shame in the world, for their cruel minds against the truth, and punishment at God’s hand, deserved for their deserts. Let the experience of the time past be a confirmation against future fear.

¶ Because thou hast a little strength: The common translation has, because thou hast a little virtue, the sense, if I be not deceived, being well expressed which depends on that which follows, neither is it absolute of itself: as though he should say, because although thou hast but a little strength, yet thou hast kept my words. And in deed the fortitude in the greater danger is more famous. And this manner of speaking is frequent among the Hebrews, who use the copulative use, for the discrete particle: (the custom and manner of which is frequent with John) as, Neither shall any straw be given you, and ye shall deliver the whole tale of brick, for, yet shall ye deliver &c. Ex. 5.18. So, And behold an escaping remnant in her, for, yet shall some remain who shall escape, Ezekiel 14.22. Afterwards also John in the same manner, And men raged in heart, and blasphemed and repented not, for, and yet repented not, chapter 16.9. If he had prayed a part their small strength, how should there not be in the same thing much depravity. For this is wont to abound, where that which is opposed, is but little and small. Sardis had few names, upon death had possessed the greater part. Neither would the Spirit have passed over in silence the corruption, if he had found any worthy reprehension. Therefore the common translation ought here to hold in that sense which I have shown. This Church is of weak strength, which dwelleth here and there, and the greater part under a popular state, one only people enjoys a Monarch for their patron. But neither is this Church able to do much either by her own or by her friends’ riches. Therefore the greater is the praise of thy fortitude O Philadelphia: who hast not yielded to the threats of the adversaries, neither forsaken the truth, by being dismayed with the vain fear of men.

1 Behold I give of the Synagogue of Satan; Here is a defect of the word some, I will give some of the Synagogue of Satan, of those which say that they are Jews. This is the future good thing, as we have shown in the Analysis, and it may be manifest from the latter member of the verse, Behold I will make them come: unless perhaps this verb of the present tense diminished, respects the present time, wherein some of the Jews submitted themselves to this Church, for a token and pledge of a full submission afterward, which it may be the last words mean. We showed upon the ch. 2.9. how they which by nation are Jews, do lie saying they are Jews, to wit in bragging that they are the only people, when meanwhile they refuse Christ, in whom only we are counted children, and do continue and rest in the abolished ceremonies of the law. By which things they have made themselves to be the Synagogue of Satan, and not a congregation of saints, whatsoever they affirm to the contrary in words. In the Antitype are Jews as many as entangled in errors, challenge to themselves alone the truth, faith, salvation and promises of God, speaking of nothing, but the temple, the temple, of which sort were the Arian Bishops under Constantine, Constantine and Valence, and such as are at this day the Romanists, glorying no less in the Circle of Peter, then of old the Jews in their temple. These only will be Catholics: their Church to be the only spouse of Christ, that no salvation can be found, out of their congregations. But let them deceive themselves with as good words as they will, by their true name they are false Jews, in show only Christians, who gather congregations in the honour of the Devil: God acknowledges them not, which thrust upon him another worship, than that which he hath appointed from heaven. Some of these therefore are given to this holy Philadelphia, seeing there are many daily, whom God of his singular mercy plucketh out of the jaws of Antichrist, & enlighten their eyes, that they may acknowledge & embrace the truth. Among which are Peter Vergerius, Peter Martyr, Hier. Zanchus, Martinegus, & many other, both Italians & other nations: who first being papists were afterwards converted to the truth.

¶ Behold I say: Excellent undoubtedly was once the victory of the Philadelphians over the Jews, and no less famous shall be at length the triumph of this Church over the Papists. Hitherto we have fought with them by pen and ink: but the time shortly cometh when they shall be rooted out by weapons, chiefly by the labor of this Church, as will be shown more plainly. Rome shall be destroyed by some other means, but being overthrown, holy Philadelphia shall uproot the remnants of the Popish kingdom so that no name of it shall be left, as we shall show in chap. 19. For this worship of the false Jews pertains to that time when the Roman beast is cast into hell; all his hosts shall be killed with the sword that comes out of the mouth of him who sits upon the horse.

¶ And they shall know that I have loved you; For until now you are made a mocking stock, neither do unthankful men acknowledge any love of mine, by the singular gift of godliness, which I have bestowed on you: But then I will adorn you with those things also which are in account with the world: you shall set up a token of victory over your enemies, & shall enrich yourself with their spoils, that every one may be compelled to confess that you are dearly beloved, who, contrary to all hope, they shall see increase so wonderfully. O holy Philadelphia, cherish your hope with these things, neither be grieved in mind whatsoever the world says otherwise.

10 Because you have kept etc. My words and doctrine, which I have taught the world with great patience, and which is also to be preached always with the same patience: which I see you have used to your great peril, and yet you have remained constantly in your duty.

¶ I will keep thee also &c. But what is it to keep from the hour? Would not God suffer the temptation to touch the Philadelphians at all? It could scarce be done that they should be free altogether in the common calamity of all the world. To keep therefore is to deliver, as the Lord did keep them out of the hands of their enemies; that is, delivered, Jud. 2:18, as though he should say, I will not suffer thee to be overcome in that temptation, but I will give thee strength, by which thou mayest not only bear consciously the calamity, but also overcome & be victor. But what is this hour of temptation? In the type itself, that persecution doubts under Trajan, which Philadelphia together with all the other Churches sustained. Neither is it to be omitted why in the Epist. to the Ang. of Smyrna, he said that the same affliction was of x days, which in this place he included in one hour: in both places he respects the concurring of the type & antitype: there because under Constantine, Constantine & Valens (within which times we have shown that the antitype of the Smyrna Church is to be limited) there should be a long calamity, raging in the greatest part of that space, he defined that affliction by x days; in which he noted both the years, so many as Trajan should go on with rage, & also that long delay in the antitype under the Christian emperors; But seeing in the antitype of the Philad. Church there should be affliction far greater than all, yet short, he has joined the same trouble of times in one hour in the type. This temptation therefore yet to come, which shall come upon the whole world is the last fight of the Roman Antichrist in the west, & of the Mahometan Turks in the East; very terrible in the whole preparation; but on which the Church shall carry away the victory, to be preferred far before all the triumphs and the victories of all men. Of which is here given a taste the full declaration is reserved to his own place.

But seeing in this battle there shall be a common victory of the whole Church, and here seem to be promised something proper to this alone, perhaps this temptation shall be another, which shall go before that war. And before we have heard that in the Church of Germany some grievous thing doth hang over their head. For he threatens that he will come as a thief; then also in the Church following we shall see that some storm is to be expected. Wherefore it is to be feared that shortly this temptation will come upon us and shake the Christian Churches with a horrible tempest. Besides the conjecture of this place, the sins which reign everywhere, not without cause indeed may increase this fear. It shall be profitable for everyone to prepare himself so that he may stand firm in that day. And we may guess at the greatness of this tempest in some sort from the very words themselves. For they promise that this alone shall be kept pure, sound, and undefiled, to which also belong the reward of Pillars, verse 12. What then shall be done with the other Churches? The future disturbance of all things seems so miserable that there shall be no face of any Church anywhere besides. For it seems that those Churches at last shall by the just judgement of God come to nothing, which have not undergone full reformation.

11 Behold I will come quickly: Until now the good thing: the way to preserve is by constancy, unto which he exhorts, first by his quick coming. The Philadelphia Church felt the hour of temptation, later after this writing. For Trajan succeeded after Domitian: under whom John received this Revelation. Neither shall the newly restored Philadelphia find it to be long, before all these things be performed. Within two hundred years after she was born again, she shall see the issue and end of all these things, as the prophecy following shall declare with God his help.

¶ Hold that which you have, that no one may take away your crown: Go on courageously in the race in which you have begun; keep your sanctity of manners, purity of wholesome doctrine, severity of heavenly discipline, lest if you begin to relent in any matter another takes your crown from you. But what crown is this? The honor which she shall receive from the enemies brought under her and worshiping before her feet, ver. 9. These manners of rewards depend on the duties of godliness, to which they are proposed, and are sometimes taken away from the saints for a correction of their cowardice. Therefore they are unskillful who transfer these things to eternal life, as though that could be taken away from the elect, or at least, as though they should always waver as to an uncertain and doubtful thing, of which they could have no sure hope as long as they dwell on earth. It may come to pass, and it always comes to pass, that the wicked may deceive themselves with a false persuasion. But the elect have the Spirit, who witnesses that they are the children of God, neither can He, the author of all truth, either deceive or be deceived, Rom. 8:16. Although if any think that there is the same reason for the earthly and heavenly reward, and that they will have that to be at least a type, the same thing may be answered truly and rightly, which we have said before touching the book of life, ver. 5: that many are called, but few chosen. Now the crown may be taken away from those who are called but not persevering, who for a time did hope for it; in this respect it is called, not without cause, their crown. But how trifling is it that they wrest unto the elect that which pertains to the called only, because they envy that others should have the certainty or assurance of salvation which they themselves feel not! As to the words, “take it” is here the same as that of Matt. 5:40, “and take your coat,” that is, take away.

12 He that shall overcome, I will make a pillar; word‑for‑word in the Greek, “He that shall overcome, I will make him,” or, as touching the overcomer, “I will make him”; a Hebraism of the nominative case absolute, such as we have observed in chapter 2:26. The reward is that he shall be like a pillar in the Temple of God, that is, he shall abide firm and stable in the Church of God, neither shall he fear any ruin or fall, in whatever manner the rain shall fall, the floods shall come, and the winds shall blow, and all things at once shall fall upon it. He alludes to those two brass pillars, placed in the Temple by Solomon, which did illustrate the stability of the children of God, 1 Kings 7:15. And so is this Church, by the grace of God, not defiled with schism and foul apostasy, as lately we have seen in the Sardinian Church: which, taking no care of a full reformation, by the just judgment of God lost many citizens, losing them as a fig tree’s unripe figs, so far, they should be a pillar. Philadelphia should be free of this sorrow, not because she shall see some apostates, who shall feign godliness for a time, but because those few should more commend her faithfulness in trying and casting out hypocrites than cast upon her any blot of schism and defection.

¶ Neither shall he go out anymore: The pillar is declared by a double property, one of continuance, another of a name written upon. The first is signified in these words, “and he shall go out no more,” the force of which seems to be this, that they may meet with a secret doubt, which perchance might trouble somebody’s mind, because when the city was taken by Nebuchadnezzar, those pillars were broken and the brass of them was carried to Babylon, Jer. 52:17. Least any should fear that the same should befall him, namely that although for a time he shall be placed in the Temple, yet at length he should be banished away, he bids them to be of good courage. For he promises that this pillar shall be such, as no Nebuchadnezzar shall ever break in pieces, neither ever carry away by any force. The Son abides in the house forever, John 8:35. The bondwoman with her son is cast out, but the heir shall live always in the sight of his father, Gal. 4:30, etc.

¶ And I will write upon him the name of my God. The name written is threefold: of God, of the New Jerusalem, and a new name of the Son; all of which are spoken according to the manner of the pillars in the Temple, the figure of which the Spirit here declares, pointing at it as with the finger, teaching that nothing was ordained in vain, although it might seem to be of never so small moment. Solomon adorned the two erected pillars with two names: the one on the right hand he called Jachin, that is, “He shall establish”; the one on the left hand he called Boaz, that is, “In him is strength,” 1 Kings 7:21; not only does the matter of the pillars themselves, but also the names, show in what firm state the elect stand before God, both present and future. For the present, the children of God have strength in themselves; for the time to come, God will so establish them by his grace that they can never fall away from him altogether. Although I may also remind you of this further, that they seem to signify the two churches: the one on the right hand, Jachin, the Church of the Jews, which God at length in his time should establish, having not yet obtained stability because of their hardened hearts, whereby they should refuse Christ when he comes; the one on the left hand, Boaz, the Church of the Gentiles, because of the present strength which should be in it when it embraces Christ at first hearing. So Christ would write names upon those pillars, better than those Jachin and Boaz. For first, he will imprint the name of his God, so that it may be manifested to all men that they have been set at liberty to be God’s chief treasure and riches, as it comes to pass in things marked openly, which show by their titles to everyone that looks at them, which they are. In that sense it was said in verse 9, “and they shall know that I have loved you.” In this respect also, holiness to the Lord is written upon the bells of the horses, Zechariah 14:20.

The second name is that of the new Jerusalem, which in Chapter 21:2, to which this reward pertains: from whence it is clear that these seven epistles respect not only the present condition of the seven cities, but, by way of types, also contain a long following age, even as we have interpreted. But as it pertains to the new Jerusalem, we will show in this place that it is not that city which the saints shall enjoy in heaven after this life, but a Church to be expected on earth, the most pure and most noble of all that have ever been hitherto. The rewards in a peculiar manner serve the times, and if this felicity shall be after the resurrection, it shall be common to all the saints, not only to this Philadelphia. This therefore signifies both that the Philadelphians shall continue until that restoration in which the new Jerusalem shall come down from heaven and shall be conversant with men, and also shall be joined with the same in a league and fellowship, be endowed with that heavenly city, and enjoy the same law, privilege, and happiness. At that time all shall acknowledge their reformation not to be a thing devised of man, as contentious men affirm, when they shall see the same ordinances flourish in the new Jerusalem.

The third name is the new name of the Son: What can be new to him? Namely that which is not yet acknowledged by the world. Hitherto he has suffered the tyrants to bear rule and to tread upon the name of Christ, as though he were a King only in title, who should have the right to reign but lacked power. But at length he shall rise up, and shall take a club in his hand: he shall destroy all his enemies, he shall give the triumph to his spouse, and shall be celebrated King of Kings by all men throughout the whole span of the earth. To the society of whose glory he shall take his servants, he shall deliver them from the calamities with which they are now oppressed, he shall give them power over their enemies, and shall bestow on them the whole glory of his kingdom, as much as mortal men can receive. And there is some difference between a new name put absolutely, as in Chapter 2:17, and a new name of the Son. For that pertains to the certainty of adoption by Christ, which faith was very weak in the Pergamene state; this belongs to the society of the kingdom, which shall be communicated with him in the last times.

13 Let him who has an ear hear; hear Philadelphia and rejoice, you are low and unesteemed, but God will exalt you. Only go forward constantly and augment your care and diligence, slake and assuage it. Neither regard the scoffs of the wicked, who will bring upon themselves sorrow and a crown. Shortly there will be an end to your warfare. In the meantime we will pray for your peace. Do again join your prayers with ours, that Christ would bestow the same blessings upon the rest of your brethren, which he has so greatly approved of you. Farewell. The grace of our Lord Jesus Christ be with you, Amen.

Analysis.
So is the Epistle to the Philadelphians, the last remains for the Laodiceans, whose inscription is to the angel, like the former. The description of him, by whom it is sent, is fetched from a double property, first of Truth, partly in the promises, in that he is Amen, partly in the Doctrine, in that he is the faithful and true Witness; secondly of power, whereby he is the beginning of the creature of God, ver. 14. The narration first reproves and shows the greatness of sin, both secretly omitting any mention of good, as in former churches, and also openly, both by comparison of coldness, as a lesser evil, ver. 15. and also by the punishment to be inflicted, the vomiting from his mouth, ver. 16. After he teaches the way to heal them, both by opening the cause of the disease, which is a false persuasion of their own worthiness, and ignorance of their misery, ver. 17. and also in prescribing a remedy to be sought from Christ alone, ver. 18. And not this alone, but also by persuading its use, as well as by chastising sons if they neglect it, ver. 19. as also by his readiness to apply, ver. 20. and by the reward, ver. 21. The last end is the epilogue, to hear what the Spirit says to the churches, ver. 22.

Scholions.
14 And to the Angel of the Laodiceans: Laodicea situated at the river Lycus was once a great city and famous, abounding both in citizens & riches, and also in all other things, as we showed in the first chapter, verse 11. It was built by Antiochus, the son of Stratonice, and for his wife Laodice, on her behalf, called this city Laodicea, as it were, the Princess and ruler of the people, to whom she should administer justice and make laws. From whence we call her Glorious, great both by name, and also in their own opinion, which boasts that she is rich, and wants nothing, verse 17. It is from Philadelphia more toward the east than the south, being distant from it according to Ptolemy not above a tenth of a degree. She is the third city since there was mention made of Jezebel, the reproach of whom Sardis took away from the churches. She has this property to her, that she has none, to whom she can be opposed, as in the former churches. To Ephesus was opposed Thyatira, to Smyrna Sardis, to Pergamum Philadelphia, Laodicea the seven have no fellow. The Antitype is the third reformed church, which before I note or show, the unjust suspicion and offence of some men is to be put away by inter‑treaty. No disease or corruption of mind has moved me to seek out an odious application. No man’s either riches or honours, God is witness, grieveth me. I am content with my little. Neither have I counted anything to be more foolish, than to please one’s self by displeasing others. But how dishonest and filthy a thing it is, to sit as the fly upon the sores of the brethren? My soul has always abhorred such dealings. But when I considered that these seven cities were set forth for a type of all churches among the Gentiles, and then also perceived the course it itself of the time, and the marvelous concurrence of all things, I did not unfaithfully hide the truth with silence, lest I should make myself guilty of others’ blood. Far be it, that I should disdain willfully that church which through the mercy of God has brought me forth, nourished and sustained me, which I desire in my daily prayers and labour, to be most blessed. But seeing the sore cannot be cured, unless it be touched, neither truly touched without grief, I thought I must not refuse to cast myself against what troubles so ever, rather than to betray the salvation of her, of which every one of us ought to have greater regard and care than of his own. Truly he that gathers the tears of his children in his bottle knows that I have not viewed round about this Laodicea with dry eyes. I could not but mourn from the bottom of my heart when I beheld in her Christ loathing us, and very greatly provoked against us. Therefore let no man blame me for that, which is not so much my will, as the duty of a faithful interpreter compels me to bring forth. And I hope that the lovers of the truth will not despise and refuse such equal and reasonable request: with which hope supported, but especially with his aid, who is the leader of my way and life, I will gird and make myself ready unto the thing itself. The Antitype I say is the third reformed church, that is, ours of England. For all the purer churches are comprehended in this trifoliate difference: for either they persist and continue in those steps which Luther has traced out, such as are the churches of Germany, especially of Saxony, and those next bordering Switzerland and Denmark; or they abhor that error of consubstantiation, as all the rest with one consent: which yet does not agree in all things, but follow a differing manner of governing and administering, the French and their companions one, our English another, a certain propre and peculiar one. Whereupon there are three distinct severally, unto which the three types Sardis, Philadelphia, Laodicea, after that Jezebel was overthrown, that is the yoke of the Roman tyranny shaken of, does answer. And to the last Laodicea, the English do agree, whose last original took her beginning at the year 1547, when Edward the King of most famous memory, came to the rule and government of the commonwealth, but then at length she was confirmed and established, when eleven years after our most peaceable Queen Elizabeth began the kingdom. Most mighty King Henry, his father, had expelled the Pope, but retained the Popish superstition. And before he began to stir any whit, even against the Pope, the churches of Germany and Helvetia were founded. The Scottish church is later in beginning than ours: yet by right it is numbered with them, with which it agrees in ordinances: into whose times she is cast, which is to be esteemed rather from the agreement of things, then alone from the difference of time. Therefore our English church alone constitutes the Antitype answering to Laodicea; as she which began last of those, in which there appears no difference of any moment.

¶ These things say that Amen: Amen is used as a proper name and is unchangeable, as before “He that is, He that was, and He that comes.” This threefold property pertains to it, that it may teach how Christ would present Himself in governing this Church. The first is taken from the first chapter, verse 18. Although “Amen” there lacks the article, and neither is it read by the common interpreter at all, yet notwithstanding this place gives conjecture that it ought to be read. The second is taken not from the same chapter, but from the common Epistle, verse 5. Neither is the third found in explicit words, but in verse 8 where He is called “the beginning and the end,” from which this seems to proceed, the beginning of creation. The first two properties pertain to the double truth, one of promise, the other of teaching: in respect that He is called “that Amen,” according to the Apostle, “In Him are all the promises of God, yea and amen,” 2 Corinthians 1:20. In respect of this, He is a faithful and true witness.

As such, Christ takes this name upon Him now because He should show Himself very clearly and be famous for performing His promises. But what are they? All blessings of heaven, earth, cattle, children, peace, warfare, good health, and the like, to those who obey the voice of the Lord; but all contrary things to those who refuse, Deuteronomy 28. Which, how they were performed to the Laodiceans, is not plainly apparent to us, as we are destitute in this point of view of history.

As touching our England, nothing can be more clear than the excellent goodness of God in this thing. For the space of these forty-two years and more, what abundance of all good things has been poured forth upon our island! He has given us a most peaceable Queen, excelling so in all praise, as no age has seen the like. Together with her He has given peace. What good thing has not issued from thence? From hence the laws are in force, judgments are exercised, every one enjoys his own, injuries are restrained, wantonness is repressed, the nobility is honored, the common people go about their work with all diligence, arts do flourish, handicrafts are used, cities are built excellently, riches increased, infinite youth grow up, the fields abound with corn, the pastures with cattle, the mountains with sheep. What need I use many words? Hence is a port and place of refuge opened to the banished for Christ’s sake, affords aid to those oppressed by tyrants, neither have we almost any other labor than that we may help those who need, and all this even while our ears do ring with the noise and tumult of the nations round about us, no less than the waves of the sea. England never had so long quietness of days, at which our felicity strangers are astonished, our enemies are grieved, we ourselves almost know it not. But praise be to Thee, most true Amen, who has given us this ease and rest. In bestowing largely upon us so many good things, Thou hast shown truly to the world that Thy Gospel is a guest not going away scot-free, which doth so abundantly bless those that receive and entertain it. Keep and continue these good things unto us, yea Thou wilt keep them, who art Amen, if we shall keep and defend Thy truth.

¶ That faithful witness is true: The second attribute is truth in teaching. These things pertain to the prophetic office of Christ, as has been said in the first verse of the first chapter, where he is called faithful because of the diligent work with which he carries out his office with great faithfulness, to whom the Father has entrusted a matter of great importance; this is true for the soundness and sincerity of speech, without any, even the slightest, trace of falsehood.

In this kind of truth He should manifest Himself in a wonderful manner in this Church.
But regarding the city of Laodicea, we have no more to say than before.
In the Antitype, those former riches of His grace are, if it may be said, surpassed and exceeded.
And to what end were all the good things if we could not have the wholesome doctrine of truth?
But ever since the first years of our most peaceful Queen, He has continually raised up diligent and learned pastors and teachers who have preached the word purely and sincerely.
Even today, many, by His infinite mercy, bestow all their labor on imparting to His people the whole will of God, pure and uncorrupted by any leaven of falsehood.
Although not without cause indeed, one may marvel how, in such disorderly custom and license to do all they will (except defamation of dignities), the doctrine has continued so long, whole and sound.

But He who is a faithful and true witness sanctifies the pastors with truth beyond all hope: in whose lips He dwells even now; although by many obscure tokens He threatens that He will go away soon, unless He is met soon.

¶ The beginning of the creature of God: the last property which is of power. For whether we interpret the Greek word for beginning or for dominion, it comes to the same end, seeing it is necessary that all things be subject to His government, who in the beginning made them. In this respect, Christ has shown Himself wonderful also among us. What has not the Pope of Rome endeavored and undertaken, that he might trouble our peace, partly by execrations, excommunications, and bulls, sounding an alarm to open rebellion, partly attempting privately, Jesuits being sent by stealth, and other secret murderers who should kill the sacred Princess with sword, poison, torments, devilish arts, or any other way. We know that not long ago the Prince of Orange was set upon with the desire to kill him by a popish cutthroat, and was wounded. Late is the memory of Henry, King of France, whose murder Jacobus Clemens, a monk, attempted and accomplished. And Henry the Fourth, who now enjoys the sovereignty, escaped hardly the bloody hands of John Castell the Jesuit, being stricken through the jawbone with a knife, and two of his teeth dashed out. But our Queen, assailed by many at many times, with sundry treasons, has been kept whole and sound from the least harm. From whence was this, I pray? Was opportunity wanting to these wicked men? The only Prince of the creature, to whose beck all things obey, has laughed to scorn and deluded the counsels of the wicked, repressed the endeavors of the ungodly, and made frustrate their subtle devisings, and restrained them lest they should touch His anointed, nor hurt the nurse of His Prophets. His power is no less famous in bridling the Spaniard, with whom we have been at war now for so many years. What is there that He does not think to effect by His riches, who alone procures trouble almost to all Europe and other parts of the world? The invincible navy of the year 1588 swallowed up in hope our whole country, our lives, and goods. But, Good God, how was it disappointed without any labor of ours, through all the seas cast asunder, scattered here and there, and broken in pieces? It came out one way against us, and fled seven ways before our face. This is Thy praise alone, O most mighty Governor, whom the winds, the waves, the hearts and hands of men will, whether they will or not, obey. O ye Kings, why do ye not regard? Why do you not learn, ye that judge the earth? Will ye fight yet still against the Prince of the creatures to your own destruction? If ye shall go on to be so made, we in the meantime will betake us under His wings, by whose defense alone we stand safe against all your assaults. Such is then the threefold property whereby Christ shows Himself to be seen in this our Laodicea, to wit: constancy in promising, sincerity in teaching, then an invincible power in defending.

15 I know your works, that you are neither cold nor hot. In declaring the greatness of their sin, He makes no mention of any good thing, contrary to that of the other churches, none of which was in such a desperate state, not even Pergamus nor Sardis, as to be void of all praise. But this evil, as though it could not endure the fellowship of any good thing, hears nothing but reprimand, without confirmation of any honesty. Not that there were not many singular men, whose faithfulness and diligence the Spirit might approve (for it cannot be but that where Christ is a faithful and true witness, there some should take singular pains), but because He respects the common form and outward face of the Church, namely, of what quality it is, not so much for its own sake, as for the administration of the Angels, which was such that he who considered the matter but with indifferent eyes would judge it worthy of being void and empty of all virtue. It is a horrible evil which refuses all fellowship with goodness. And although by this silence we may be able to conjecture how grievous the disease is, nevertheless afterward it is described more plainly of what quality it is, and first, for more clarity, by a denial of contraries: “I know,” says He, “that you are neither cold nor hot, but something compact and joined together of both.” Whereupon this evil consists of a temperature and mixture of certain contraries. Now He called him cold, who with a quiet mind can endure that the duties of godliness should be neglected and despised, little or nothing at all regarding what manner of worship either he himself or others hold. He called him hot, who boils with a strong affection and desire through vehement heat and fervency, as scalding water seething in the pot with a certain restless motion, for so the Greek word zestos signifies, of which sort are those who can by no means suffer superstitions and ungodly religions, but do try all lawful means, that there may be an amendment. For hot is not here sinful, as a rash zeal, as it comes to pass in habits, in which both extremes swerve from the right; but it is of praise, as Apollos being fervent in spirit, Acts 18:25. And Paul exhorts that they be fervent in spirit, Rom. 12:11. If by excess he should degenerate from the truth, lukewarmness, holding the middle, there was some consideration of honesty. But fervency or zeal is an affection, following the love of holiness, with a great and earnest affection of mind; whose defect, whether that more removed from coldness, or this nearer to lukewarmness, is blamed. And lukewarmness, placed in the midst of these extremes, whereby a man, staying himself from committing grievous sins, embraces godliness so far as may be enough to maintain the reputation of an honest, prudent, and civil man. The college then of the Laodicean pastors was, as it were, a senate of prudent and moderate men in the matter of religion, even as at this day the lukewarm have the common report in every place. Yet it is not plainly mentioned from what mixture of things this lukewarmness arose. Before these times of John, Paul bids the Colossians say to Archippus, who then was the pastor of the Laodicean Church, that he would look to fulfill in the Lord the ministry which he has received, Col. 4:17. From which it appears that pastoral faithfulness began then to shake and lean, which afterward fell most shamefully when the Spirit sent these epistles to the angels. In our England, the matter is clearer, where there is such a form of church established, as is neither cold nor hot, but set in the middle and made of both. It is not cold, in as much as it professes the healthy, pure, and entire doctrine of salvation, whereby we have bid farewell and forsaken the Romish Antichrist, and have risen from that cold death wherein we lay before. Hot indeed she is not, whose outward government for the most part is still Romish: in the degrees of their clergy, in elections, ordinations, and whole administration of the censures. This mixing of the pure doctrine and Romish regimen together makes this lukewarmness, whereby we stand in the middle between cold and hot, between the Romish and Reformed churches, of both of which we are compact, as Martin Bucer, of godly memory, complains in a certain epistle sent to a most beloved friend of his at Cambridge, written January 12, 1553. He, in the times of King Edward the VI, was used among others who should determine the reforming of our church. But in what things both his own and Peter Martyr’s authority prevailed, he himself manifests in that epistle even now spoken of: for so he writes, “Whereas you put me in mind of the purity of the rites and ceremonies, know that no stranger is asked concerning those things; yet of ourselves, when we may, we fail not to do our duty by writings and in presence, and chiefly that the people may be provided with true pastors, also of the most purity, both of doctrine and ceremonies.” And in another place: “There be some who by most human wisdom and vanishing cogitations would join together God and Belial, by the leaven of Antichrist.” These are things he did write, which we today find by experience too true.

¶ I would that you were cold or hot. I would to God that you were either wholly Roman, or at length admitted a full reformation. He shows the horrible greatness of the evil by comparison, wherein he prefers a wicked and no religion before this mingled lukewarmness. But does not lukewarmness come nearer to good? From whence then has it more fault? Certainly sin is more sinful where grace is more plentiful. The fall of the angels in heaven, left to themselves, had no way to obtain pardon. The sin of our first parents was more wicked being committed in paradise; most foul was the idolatry of the twenty-five men committed between the gallery and the altar itself, Ezekiel 8:18. God will be sanctified in those who approach unto him, and suffers more easily His grace not to be known than to be despised. The servant that knows his master’s will and does it not shall be beaten with many stripes. Wherefore, if Baal be God, follow him; why halt ye between both? As though it were hard to judge whether it were better. God abhors to come into this trial. There is more sound judgment in him who, not knowing the truth, continues in his superstition than in him who, being somewhat enlightened, is tossed this way and that way, uncertain still what to follow. Therefore a mean here is worst of all: which, under a show of prudent moderation and tranquility, is honored by the world, which God esteems less than His next extremes on both sides. Is it then better to fall away to Rome? Far be it from us. For in this place Christ prefers the blind Papists before those angels who, bewitched with ambition and covetousness, refuse holy reformation. He says not that the condition of the whole Church is worse, to which the true food of salvation is ministered, of which no power is granted in the Roman Church.

16 Therefore, because you are lukewarm, etc.
The anger also of the punishment discovers the horror of the sin, which seems to be confirmed by another;
For the Greek word which Theod. Beza translates, therefore the common Interpreter has it, but it is a single swearing and confirmation by other in this place, as though he should say, So, or thus let this or that be done to me, as it is certain that I will vomit you out of my mouth,
After which the word ‘So’ is used by the Latinists, as in that ode of Horace. So the mighty God of Cyprus, etc., as it has been observed by Henry Steven. And with the Hebrew ‘Amen’ is the same with sic, as in Isaiah. So he bore our sorrows, that is, certainly, chapter 53:4, and Ecclesiastes chapter 8:10. And so I saw the wicked buried, that is, truly, certainly, as some would. And such silence is often used in execrations; Therefore I swore in my wrath, if they shall enter into my rest, Hebrews 3:11.

¶ It shall come to pass that I will vomit you: as it happens with meats, which either hot or cold are retained in the stomach because of their exceeding quality, which causes sensation and excites the stomach to embrace them; but that which is lukewarm, because of its near and familiar heat, is neither felt upon entering, nor being entered is it for that reason digested, but remaining idle, and eventually causing trouble by its lingering there, is thrust out of doors with vomiting as an unprofitable guest. But we must beware that similitudes are not twisted beyond what they intend, as though naughty and wicked men should remain constantly in Christ as cold meats remain in the stomach. For such were never in Christ; neither does he indicate what he approves simply, but what he prefers. Furthermore, the matters are referred to his external administration, whereby he bears longer with the notably negligent, or rather all strangers altogether, than with the lukewarm, as the experience of all times proves, and at this day we see in the Roman Church, which although she has utterly forsaken the truth, has flourished a long time, while in the meantime God rebukes immediately the true, and does not delay chastisement to any long time if he sees them slacken their earnest affection and lean more toward lukewarmness. But what is it to be vomited out of his mouth? Will Christ, in whose mouth and lips the very truth rests and abides, take away his truth from this Angel, delivering him into absurd opinions, so that he should believe lies again? The itching desire of many men at this day to give again to the people monstrous and rejected opinions makes this interpretation probable. We know what has been taught within these few years in the Schools, is preached usually in the assemblies, is disputed at the public Comices, and was published in print last summer. But this should be the punishment as well of the people as of the Angels, to whom it seems to be proper. Therefore I have no certainty regarding this matter. Surely the event will declare it shortly. In the meantime, let us know that this shall be a fearful punishment: for first, Christ will take great pleasure in rejecting from himself this Angel. For what can be more pleasant to a man who has a disposition and will to vomit than to be immediately relieved of the cause of his grief? Even as Moses threatens the apostate Jews, that Jehovah will rejoice in destroying and rooting them out, as he once rejoiced to do them good, Deuteronomy 28:63. Secondly, because he will cast out this Angel with great dishonor. For an unclean place is sought for vomiting; however, Antonius in the assembly of the people of Rome, governing the public business, filled his own bosom and the tribunal with gobbets of meat. Thirdly, that the Angel shall never recover his former dignity. For far be it from the Prince and Author of all cleanness to ever return to his vomit. But this punishment was not to be inflicted on the whole Laodicean Church, but on the Angel alone, that is, on all lukewarm pastors, partly because of what we have just spoken, partly because the Church is usually mentioned expressly when treated of. As to the Ephesian Angel, “I will remove your candlestick out of its place,” Revelation 2:5. It shall therefore be peculiar to the ecclesiastical men without the destruction of the whole Church. Neither is it to be doubted but the same eventually happened to the Laodicean Angel, which here is denounced, which thing is also certainly to be expected in his Antitype, unless she shall prevent it by repentance. For it shall come to pass that that faithful witness shall overthrow this whole hierarchy, and not always suffer men seeking only honors and riches, not those things which are Christ, to enjoy even this false felicity. Certainly a great and reproachful judgment abides those lukewarm ones, of whom, though they be troubled with no fear, as having put to flight all the noise thereof, yet though all shall hold their peace, he will not deceive, who has threatened that he will punish. It is also to be feared that the Church may feel some adversity through contagion and consenting to. Such as are the Angels, such does she become for the most part; and none is so ignorant of the matters who does not plainly see that the whole body is sick of the same disease. But have mercy upon us, O thou beginning of the workmanship of God; deal not with us according to our sins, thou knowest our making, that we are dust and ashes. How should not the earth grow cold? Raise up in us the burning heat of thy love; dissolve, I pray thee, our ice; neither suffer us to please ourselves in our imparted godliness, but kindle us with thy heavenly fire unto full heat and fervency, that we may both avoid thy loathsomeness of us, and may always enjoy that pleasantness which thou givest to those whom thou lovest: Amen.

¶ For you say, I am rich: thus was the nature of the sin. The cause is double: a false persuasion of their own worthiness, and ignorance of their misery. That grew from their wealth, which was earthly and not spiritual riches, for against these he opposes the riches which he bids the Angel to buy of him in the next verse.

Neither could he have been lukewarm if he had expected spiritual riches from anyone other than Christ alone; rather, he was thoroughly cold, and altogether a stranger to grace, having become void and separated from Christ (Galatians 5:4).

But he seems to have abounded in earthly riches, because of the wealth of the city which we spoke of (Revelation 1:11). For which cause, perhaps, Archippus was more negligent of his ministry, whereupon Paul would have admonished him (Colossians 4:17), although small fruit seems to have followed that, seeing that even unto these times of this Revelation, there was such great matter of boasting, and that also not newly bred, but gathered from old times.

The abundance therefore of things for this life begat this lukewarmness. And it is no new thing that prosperity steals away our minds and draws men away from God. This warning is often in the law, that they should take heed of themselves lest, being fulfilled and filled with good things, they should forget Jehovah. And the boasting is threefold: the first of the present wealth; the second of long continuation; the third of perfection and absolute sufficiency for every use.

For so the words require that “I am rich” should refer to the present riches; “I have been rich” to those past; “I want nothing” to a certain fullness. From which further must needs spring a certain persuasion of a permanent state, and also constant felicity for the time to come. And it is to be observed that he brings in this Angel boasting in his own words, otherwise than was done hitherto; yet this not in vain, seeing nothing is uttered rashly of the Holy Spirit.

But as to the Angel of Laodicea, a clearer application offers itself: in our England, the congruency is so manifest that nothing could have been expressed more vividly. For what other cause can we attribute our lukewarmness, the Popish government mingled with the pure doctrine, than the love of riches and honors? Men will not allow this hope to be taken from them, but they would rather have half‑godlike together with the enjoyment of their riches than a full and perfect reformation with the loss of them.

Yet lest they should seem to prefer anything before the truth with dishonor, they somewhat proudly praise our present happiness in published books and in assemblies, as we may see from the writings of many men which have come forth in these last years. Not without cause therefore does the Spirit make this Angel vaunt himself, but in the same setting before our eyes our notable glorying.

And we have said that the first bragging was of the present riches. How does our Angel triumph in this respect, and lift up the head above all other reformed churches? In other places there are poor and base pastors, almost of a vulgar state and condition, nor of any greater authority than their godliness and learning can procure to them, but our bishops are peers of the realm, superior in honor to many great states, also in riches, company of men and maidservants, in magnificence of houses, and all other pomp of the world, equal to any even the greatest earls.

How rich is the rest of the clergy? The deans, archdeacons, prebendaries, chaplains, heaping and gathering together many benefices, as they call them, do match squires at least in early revenues. Does not this amplify and greatly increase the glory of the church, that her ministers shine in garments of silk and velvet, walk in the streets with the retinue of noble men, and so drive far off the contempt of the ministry? Where can one see, after the Pope is expelled, a church rejoicing in such rich things and prosperity? Nowhere indeed; neither do I envy nor grudge it; only our rejoicing is not good. And would God that our riches served to promote God’s glory rather than hinder it; but they have brought in this miserable lukewarmness, while that we may retain them, we make no reckoning of true godliness.

The second boasting is of long continuation, for this plenty is not new, but has been confirmed now by the space of forty‑two years, with how great prosperity of all things.

Who may be bold enough to reprove the condition of this church as maimed and imperfect, which the experience of long time has approved to be most happy? Not I indeed, unless prosperity were an argument rather of God’s patience than of man’s justice.

In the third place he boasts that he wants nothing: “What do you tell me,” says he, “of other reformed churches? I see no cause why other reformed churches should not imitate ours rather than us them, seeing we are inferior to them in nothing.”

The answer to the admonition made to the parliament, p. 226: “Yes, why do you call me back to the first church? As though we were bound by the first beginnings and principles as with fetters, and it were not lawful for us to alter those things which at their first origin were not so profitable as at this day they seem hurtful,” this is in a certain apology of the government of the church, p. 81, a bold, if not ungodly, assertion to affirm that anything ordained of the apostles should be no less noxious to our churches than profitable for them, for which they were appointed.

But I remit this to the heat of contention. In the meantime, let such a man know that the apostles’ church was most perfect, and was not to be made perfect by the inventions of those who came after, but that all others are to be tried and examined by its standard. That saying of the first council of Nicaea is to be celebrated, which is: “Let the old customs hold,” and that also of Tertullian against Praxeas: “Behold, whatsoever is first, that is true; and whatsoever is later, that is false.” And it is not to be doubted that Paul taught Timothy most fully how he should behave himself in the house of God (1 Timothy 3:15). Is all that instruction abrogated for age? Should time teach better and more certain things, to which the apostles should give place?

Surely the Church, as Adam in the first beginning was purest, the farther she proceeds, the more filth she gathers, unless God extraordinarily makes the light shine out of darkness, as lately in this last age. That first Church was the Garden of Eden, as we have shown in Revelation 2:7. The Church of the following ages, compared with that, was a wide and barren wilderness. Perfection is not to be measured by the multitude of professors, or by the amplitude of riches, but by the integrity and purity of God in his institution and the abundance of heavenly gifts. Let it then be enough to praise men’s inventions; let us tread under foot the sacred truth in comparison with them.

¶ And knowest not that thou art wretched? The other cause of the evil is the ignorance of their misery. For prosperity blinds the mind of the world, so that it cannot see indeed in what state it is. Therefore in many words he declares this misery, because in so deep drowsiness, a light upbraiding would not cause any feeling. He makes a fivefold degree of it, of which the first two are as certain common accidents; the last three show the very kind of the disease. For the remedy is threefold, of gold, of garments, and of eye salve in the verse following, and teaches that the disease consists chiefly in these three things. The accidents are referred either to his own sense or to the compassion of others: in respect of that, the Angel is wretched; in respect of this, miserable. A man is wretched who is consumed with some great sorrow, whether it arises from a public calamity or from some private and domestic grief. And there is none placed in any dignity whatsoever who can keep himself from this anguish, whereupon kings in tragedies lament that they so often are wretched. Such heaviness of mind did lie once upon the Angel of Laodicea, as is at this day in our England. How, wilt thou say, where no public calamity presses? The Spirit speaks of private sorrow, as is evident from the glorying of this Angel, for which there can be no place in common mourning and sorrow. But this interior grief does torment miserably the English Angel. For how great griefs does he feel who desires exceedingly riches and honors, and cannot get them? Or at least, who cannot securely enjoy those things being gotten, whom many godly and learned men inveigh against with grievous words, and not only this, but also prove manifestly from the truth of God that such dignities are unmeet for the ministers of Christ, and that they cannot stand together with the faithfulness of pastors and bishops? How must it need be that these disturbers should be very grievous, especially seeing this opinion is now favored by the multitude, and the nobility has perceived plainly long ago the truth of it?

If one could open the breast of this Angel, doubtless he might see his heart almost consumed with this grief, however outwardly all things are joyful and the commonwealth flourishes with happy tranquility. And I doubt not but that the Angel will confess that I have touched his most inward sense in this matter. This Angel is miserable to others, not to the wicked Papists, to whom the former grief is not sufficient, but to the godly brethren, both at home and in other nations, who being free of all partiality acknowledge the condition of the bishops and other clergy, who give themselves wholly to ambition and labor for honors, to be miserable and unhappy, however greatly it may please ourselves. For what is more worthy of pity than to see brethren snared by the vain glory of the world, altogether desiring and enforcing themselves to get earthly dignities, and making shipwreck of the heavenly crown? If they had always lain in the snares of the Devil, the thing were not so much to be lamented; but after they have escaped from his snares by the wholesome knowledge of the gospel, they are entangled again in the same by this way: what godly man cannot both be grieved at their change and also bewail the common misery of us all, who by a thousand means are drawn into the same destruction? Such therefore are the accidents, grievous indeed of themselves, yet but as a flea biting in comparison with the disease itself, which now let us touch as gently as we can, with the mind only to heal and not to exasperate it. The first matter to be purged is poverty. And knowest not, says he, that thou art poor? Of what sort of poor? Not the poor in spirit of whom Christ speaks, Matthew 5:3— for this is a blessed poverty—but a wretched poverty. Also, the Angel boasts that he is and has been rich, and that he wants nothing, so that he is far from that holy humility. This poverty therefore is the timorous beggar’s, which both quakes at the sight of a richer man, nor either speaks or does anything but to the pleasure of a mightier man, and also sustains the wretched life by begging money and relief. For the Greek word ptakos, “poor,” has the name both from fearfulness, and also is noted with the same name of him that, lying at the gate of the rich man, desired to be filled with the crumbs which fell from his table, Luke 16:20. Which of these agrees with our Angel? Is not all this dishonest covetousness far removed from the great riches ministered to ours? I would to God it were indeed, but here, as always, I am compelled to admire the infinite wisdom of God, who has opened our secret imposture with a word so fit for the thing, as nothing could be spoken or thought more fit. For first, how servile a fear possesses the Angel, from which may easily appear that he speaks almost nothing which he thinks may displease anyone. The bishops fear the Peers; the parish pastors, the bishops, whom they perceive to be ready to scourge them, if any provoked at home will crave their aid, especially if he can object that their mind is out of love with some ceremonies. So reprehensions are silent, naughtiness reigns, the hand of God is heavy upon us, and whither the matter will grow at last, prudent men fear not without just cause. But chiefly, the beggary of asking is notable. For run over with your eyes and minds the whole clergy. Will you that we begin at the weakest? Those that they call curates, both in very truth and also in the judgment of all men, are beggars, in whom we may see that which was threatened to the family of Eli: men bowing themselves for a piece of silver and a morsel of bread, and requiring to be joined to one of the priests so that they may eat a piece of bread, 1 Samuel 2:36. In the rest, who through their greater abundance walk more under-propped, what running up and down? What bountiful giving and bribes? What importunate and earnest entreating? How great flattering enticements of humble service and soothing of all duties, that they may procure ecclesiastical offices to themselves? Very many fly to the King’s Court, or to the house of a most noble man, the Lord Keeper of the Great Seal. For these places are like the beautiful gate of the Temple of Solomon: in this men enter in great multitudes, and there is great hope of carrying away the penny, Acts 3:2. Others follow the States and Peers, to whom they become either domestic chaplains, or that I may say, vassals: for what cause, I pray? That as soon as any benefice, as they call it, shall happen to be void, they may enjoy the same by the gift of their lords. And this is thought to be an honest way to get an ecclesiastical charge. But is not this flattery mere beggary? In obtaining a divine office, is favor any less dishonest than money? If we weigh the matter rightly, it is of the same fault and blame, to enter either by bribe or by favor. The other rabble is diligent about the common sort of patrons in the country, in whose porches they sit, flatter, and speak fair to their wives, flatter their children, win their servants by gifts, and in every place behave themselves like wretched beggars. Some more craftily, even as those who sit on a way having two paths and in public ways offer piled rods and sticks to those who travel by, so that they may get some money, so they either by bountiful giving of present money, or by agreement to give a certain yearly rent, make a way for themselves.

But you will say, this is the corruption not of our laws, but of the men. Certainly, as long as this way of obtaining ecclesiastical charges holds, which hitherto has prevailed, no remedy can be brought for this beggary. Have we not known this sufficiently by experience? In the late assembly of all degrees of the realm, a sore and heavy ordinance was made against it; has anything been effected thereby? Nothing at all, only that the thing is done more warily and subtly. We avail nothing with our laws, where the laws of Christ are not kept. But that we may proceed, when the thing is begged by the patron, how much less business remains to the unlearned route to obtain the institution of the bishop? Here not only a humble request must be made to the chief lord, but to the examiners, grooms of the chamber, clerks, butlers, yea to the lesser Jack, not because ignorance shall keep him from entrance, but because he is wont to bring the most gain to the servants, who has need of more favor. There is no tower made so strong which an ass laden with gold does not vanquish, nor almost any so unlearned or foolish who takes the repulse. But what engines and crafty means are used, let them look to it.

There is the same consideration of prebendaries, archdeacons, and deacons. Are the bishops themselves devoid of this avarice? What does it mean that they often attend at court and with the peers of the realm? Why do they not wait until they are summoned? Why are they not pulled away from their studies against their will? Yes, if anyone should appeal to their consciences, are those large estates and farms in their bishoprics let out for hire at their own discretion to farmers who desire them, or are they given bribes to the attendants of their dignity? But are they only beggars when seeking the office? Some indeed have come to such beggary that if their seat is to be changed, they do not pay their first fruits, except they have shamefully gathered some alms from poor rectors under the name of benevolence. You are therefore a beggar, O English angel. And therefore it is ordinary and usual that the best are passed over, and others less worthy are held in higher estimation. For as we bestow some alms upon the blind, lame, and those full of sores, we ignore those who appear physically well and in fine clothing; so men with a blind mind, deformed and maimed in doctrine and understanding, gather together much alms, while those with more learning and far better judgment suffer hunger and perish by famine, which comes to pass either because they cannot cry out as loudly, or because they are more ashamed to beg, or because men have less pity for them.

But it is not my purpose to plead their cause; your beggarliness, O Angel, is something I must reproach, which you will or will not acknowledge if you weigh it with yourself in earnest.
You do indeed abound in riches, but nothing is more filthy than the way you acquire them.
After a beggar has filled his purse with alms, does he cast away his patched cloak and flaunt himself in silk, pretending to be rich and wealthy? What else is there to boast about other than the bragging of riches that you have gathered most dishonestly by begging?

And yet I do not speak these things for that purpose, as though the stipend of the godly pastors, who holily both enter into and execute their office, should be mere alms. For the labourer is worthy of his wages; neither can this distribution be said to be freely bestowed, any more than it is to someone who lives on his public office. God, who made the earth, has so given it to the children of men that He reserves a portion for Himself, which He has bestowed on those who earnestly bend themselves to holy things. Therefore the patrons do not give of their own when they appoint the yearly rents to the pastors of the churches for their pains, but deliver them to those to whom they are due, and of which they have been the keepers only. We speak not, I say, of such special persons, but generally of the state of the clergy, the manner of which is so ordained that the Angel manifestly grows rich by alms, and indeed is no other thing than a lord‑beggar.

There is added to beggary blindness, whereby the evil becomes far more grievous: for what is more pitiful than a blind beggar, whom necessity constrains to seek his living abroad, and whose lack of sight prevents him from seeking? But this is a blindness of mind, whereby a man, being deprived of a witty and prudent mind, cannot provide for himself touching things profitable and honest before God and men. The Angel then, being void of this wisdom, sins even so in administering his office as he sinned by beggary in the manner of getting. And this is the worst kind of blindness, which for the most part neither acknowledges his own darkness nor can suffer admonition patiently; yea, he uses the staff whereby he ought to have tried the way, against him that shows him the danger.

Yet you are to be admonished, O miserable Angel, however froward and angry you shall be: it may come to pass that at length you may see and be wise; if not, at least I may be without danger of setting a stumbling block before the blind, if I have seen the pit and not shown it to him. And that I may deal with you more favourably, I will make yourself judge whether you be better sighted than I accuse you; although this be unreasonable in one’s own cause, wherein you must needs be twice blind. Call therefore to remembrance with me your last constitutions, which are wont to be wisest, handled in the Convocation at London and published in the year 1597.

What medicine do you make for the Church being sick? First you decreed that fit men be admitted unto ecclesiastical holy orders and benefices, as they call them. The title indeed recreated many, and very many judged thee now at length to use thine eyes. This kind of men has made the Church sad a great while. There was hope of remedy when thou shouldst see and acknowledge the disease: for of evil manners arise good laws. But how wisely hast thou met with this evil and satisfied men’s expectation, weigh well with thyself, after give sentence. You know that it was ordained in a statute of the realm that none should be admitted unto holy orders except he be four‑and‑twenty years old at least, and have brought before the diocesan the testimony of such men as the bishop knows to be of sound religion, both of his honest life and also of his professing the doctrine of our Church; yea, have been able to render a reason of his faith in the Latin tongue; or at the least has been endowed with some special gift of preaching.

Although this was long ago enacted, the Church has been greatly troubled with a new rabble of most unworthy men. With what cautions then hast thou helped the imbecility of the law? For wise and quick‑sighted men are wont, when they have perceived the weakness of the law, to help with more sharp laws for that point whereby they see the impudency of men to break through. You indeed have established many things, but I pray you, what serves for the worthiness of ministers, that no man be received to holy orders unless at the same time he shall exhibit the presentation of himself to some benefice then void? Or who shall not bring a certificate from some church wherein he may serve the cure of souls—that is, where he may play the curate under some one in reading of prayers; or who has not been appointed in some college; or at least who is not to be admitted by the same bishop unto some benefice or to a cure? To what idiot or any the worst man may not these things pertain?

But you proceed and add other things as vain as these: moreover, if he shall be, say you, of another diocese, unless he shall bring dimissory letters, be full four‑and‑twenty years old, and has taken some degree in the university (which last is required only in men of another diocese), finally that holy orders be not given except on the Lord’s day or holy days. Excellent ordinances indeed, for which the reformed churches may be ashamed. What do these things profit at all, that a fit man be admitted? What that after should be ordained ministers either more learned or more honest? Wilt thou, on the Holy Spirit crying by Paul, “Who is fit for these things?”, obtrude a man with a presentation, with a certificate, with dimissory letters, or who has been licensed on the Lord’s days?

But I will not debate the matter harder; only I appeal to your conscience: what, I pray, have you provided in this matter, who has covered the wall ready to fall with such foolish plastering? What touching plurality of benefices? You decreed that it is to be restrained. And well indeed: for it is a heinous thing that one should be a shepherd of sheep which he feeds not, or at least should receive any fruit from them who take no profit from him. It would be meet therefore that here you should bring forth whatsoever skill you have to cure this evil, which not only the divine oracles but also common sense condemns of sacrilege. What remedy then do you apply? Namely: let no man enjoy this faculty unless he be at least a Master of Arts and a public and fit preacher of God’s word. A notable physician indeed.

What have Masters of Arts deserved so ill at your hands that you would have those first burdened with so great a sin? You confess that plurality is an evil thing and to be corrected, yet you permit this mischief to them: indeed it is a notable privilege of their degree whereby they first are licensed to be evil. But whether you think that the destruction by these means would slay more secretly? There are so many, thanks be to God, as if all, hindered by no other religion, should use the liberty of your constitution, more parishes, I believe, should want pastors resident with them than at this day they want. So you do stay and repress prudently the evil by augmenting it. But perchance it is enough for you to deceive men only with a title and pretence of repressing plurality.

Moreover there is an ordinance made touching hospitality in the benefices cared for. And this is the calamity of our Church, that the ministers do not feed the poor with beef. That of binding the regulars to make sermons in their own proper persons would seem to belong to a sharper sight, unless perchance it should call them away from other places where their labour is more necessary; I let pass the matrimonial ordinances. That is worthy remembrance touching excess about excommunication to be reformed. For you see it to be defiled shamefully with many pollutions: I would to God you would see and regard as well those things which belong to the holy and lawful reforming of it.

But why do you first deny that herein anything can be innovated or altered without a great mutation to the whole ecclesiastical jurisdiction and of very many laws of this realm; yet afterward you would reduce the same to its ancient honour and dignity? Would you make a reformation without an alteration? You will have nothing to be changed, that the laws may not be violated; yet you pretend to recall the former comeliness. It pities me that you can not see your own blindness.

But by this provision you have openly shown what reform we must expect, such indeed by which no amendment may be made. Therefore the title might have been enough for this thing; yet that you might seem to do that which you do not at all, you use a certain form of ordinances. For let us see how they answer and agree to the promise. First you ordain that in grievous crimes the sentence be pronounced either by the archbishop, bishop, dean, archdeacon, or prebendary in his own person. What is this ancient use of pronouncing the sentence by those whose names, except only the bishop, had not been heard indeed in the Church as long as the true honor and dignity of excommunication remained? Why is there no place left for the pastor of every congregation to whom once it belonged to pronounce the sentence? Peradventure it makes no difference to him what is done to his sheep, or it may be that he is not fit nor endowed with judgment and wisdom enough. In very deed this feature might perchance have prevailed somewhat in time past; but now it ought not, seeing you have set us free enough from it in the first book of the Decrees.

For it is not to be doubted but that he who has been furnished with a presentation, a certificate, and the other things with which you have instructed him in the same place should be fit enough and more than fit for every part of his office. Or if I must deal with you in earnest, what would allow the pastor, using the counsel of others and making diligent inquiry, to not pronounce the sentence as well as either the bishop, the prebendary, or anyone else? But you will say, we will not have this matter handled by common advice, but will rely on the judgment of one alone. Is this the meaning of your reformation, and yet dare you make mention of the honor and dignity of the ancient use?

Christ commanded to tell this to the church: will anyone sustain this church’s position?
One indeed pronounced the sentence for the sake of order, but the matter was judged not by his sentence only, but by the advice of the whole assembly and council.
Paul would not have excommunicated the incestuous man unless the brethren were gathered together and consented, as we read in the First Epistle to the Corinthians, chapter five, verse four.
And so the church continued for some ages afterward, as is clear from Origen, Tertullian, Cyprian, and others.
I would marvel that you promise so boldly concerning the former and ancient dignity, yet I know that blind men do not fear the faces of men.
But what if this amending of yours, which you pretend, does open a way to impunity for grievous crimes?

The commissary, as long as it pertained to him, twice at least every year compelled the churchwardens by virtue of an oath that they should present wicked men; now, while he should do that, there is perhaps no cause when the priest associated with him cannot denounce the sentence against such a man. And in deed it is not to be hoped that the churchwardens willingly will flee to the bishops, archdeacons, or prebendaries whom they do not know where they may find, or who perchance are far off from them, and a journey cannot be made without charges, when being present, and that at other men’s costs they can scarcely be driven by oath to betray the guilty. You ought to have minded these things, and not used a remedy worse than the disease itself. Secondly you speak of excommunication for contumacy, which has no new thing from your former decrees. But the repeating of the old manner is with you a reformation, lest perchance any box should want a superscription although there be nothing in it. I pass by the change of penance, the foul things of the officials, the excess of apparitors (of taking away whom you ought to have intended rather than of moderating them) and registers. You yourself how may you speak how well you have used your eyes who, passing by many great evils, either are wholly occupied about trifles; or if perchance you have touched any weighty matters, you make them either worse by curing, or indeed nothing better. Certainly by many reasons your blindness is proved. But Christ open your eyes: I will not so much deal with you by words as for you by prayers. For I have not purposed the handling, but only the judging of these things. The third part of the disease is nakedness: garments are used that we may provide for shamefulness. Out of which when one is put, his ignominy is set openly in the sight of men, according to that of the prophet, “Behold, I am against thee, saith the Lord of hosts, and will uncover thy skirts, unfolding them upon thy face, that I may show thy nakedness to the nations, and to the kingdoms thy nakedness,” Nahum 3:5. Therefore this nakedness is a reproach, dishonour and contempt of which this Angel is sick. For it cannot be that our clergy should not be contemned by men who manifestly and clearly do see how beggarly ecclesiastical stipends are sought and desired, how filthily and negligently the holy offices are administered, how all care of the flock is naught set by, and the study of God’s glory is cast away. When I say men see these things, can it be that they should not despise the Angel seeking only his own things, not those which are Christ’s. And the Angel himself at certain times sees the same thing in some sort, as can testify the oft complaints of their public sermons, although he knows not the cause, or he would not know it, fearing more, as it were, the remedy than the disease. But it appears plainly how greatly he is despised from that which happened a few years since. A certain man set forth books who called himself a Marmer of Prelates, in which he dealt boldly with the Angel. How acceptable to the people were those merry conceits in words? How plausible almost to all men? How gladly and greedily and with how great pleasure were they received everywhere? No man is so ignorant and unskillful in things that, mindful of the time, he may say thus to himself, “For Jehovah has poured contempt upon the princes: those that honour him he honours, and the despisers of him shall be made light: he has made our priests to be abject to all the people, because they have broken his covenant.” These things, I say, a man considering with himself had not swerved from the truth. For if there had been any estimation of the Angel men would rather have mourned than laughed and delivered those writings to the fire before they would have worn them with so often handling and looking on them. I would not tell you these things unless the Spirit did affirm plainly that you do not know your own nakedness. That false glory wherein you flourish does not earnestly make you mind or regard what men speak and think of you. But learn from here, if you be wise, how servants going before in great number and having chains, and a great troupe of serving men following after, are of no force to drive away contempt and to deliver from the despising of the common people; or if you cannot perceive these things so well in yourself, behold the Papists and the Pope their prince: how doth he now stink for his desert with the greatest part of men, contemned, naught set by, vile and hated of all the godly; whose feet notwithstanding some princes being bewitched yet do kiss, and then whom no mortal man has been in time past of more imperial majesty. Remember our former prelates whose riches were greater than yours, their authority greater, their power more to be feared; yet because the common sort of people did see them to be mere gluttons, how did they deride them? The pride of our Wolsey was mocked openly. For the honours of this world are fig leaves, or as it were torn and ragged clothes which cover not the nakedness but make more deformed through the loops. Mind these things, and be not proud of your golden feathers, but rather where you are naked cover your shame, lest through vain boasting of the part adorned you lie despised with the common people for your other deformity. And thus at length I have opened this rotten sore; if my pains and travail shall be acceptable, and if being cleansed it does fare well, how great thanks shall I give to our God? But if the evil only shall be stirred up and provoked, and the handling shall disquiet those that are sick, I will comfort myself with the conscience of duty and the usual wages of the physician.

18 I counsel thee to buy gold from me: hitherto the cause, now the remedy is taught; both from whence it is to be fetched and by what means, and also what the matter of the medicine itself is. It is to be fetched from Christ alone; He alone has borne all our infirmities and alone yet can heal our griefs. The way to fetch is by buying: not because He requires a price; for He sells wine and milk without money or the changing of things, Isaiah 55:1–2. But because He will have a desire to be brought, even as in getting of things with great cost: in which together also He shows the dignity of the remedy, which otherwise is not dear at any price. The medicine is threefold after the manner of the disease which we have shown to be threefold: gold, white garments, and eye salve; gold is set against poverty; white garments cover nakedness; and eye salve does help against blindness.

We have said that wretchedness and misery were accidents which forthwith vanish when their fountains are taken away. Of what sort every one of them is may easily be understood by their contraries. Gold is opposed to the riches and poverty of the Angel, that is, to the hegemony of benefices and ecclesiastical offices. For the former riches are not true, and do not let but that the Angel may be the most base and vile beggar. But the gold of Christ drives far off this beggary. It is therefore the most holy manner appointed by Christ himself of calling, choosing, ordaining and appointing ecclesiastical men, each to his office; whereby pastors do not seek the office but are sought for; are not promoted for a piece of money but for goodness and virtue, not for favor but learning, not at the will and pleasure of any man but by the election and consent of his flock. Christ will have this gold to be bought from Him because He himself has described plainly this whole way and has not left it free to men to deal in this matter at their pleasure. As long as the thing shall be in the power of one patron and bishop there will never be wanting bribe‑givers and such as will suffer themselves to be corrupted with rewards. But if Christ’s rule be kept, this begging poverty would flee away never to return again. For this gold is tried in the fire, proved oftentimes and wholly refined. We see its excellency in the primitive church and also among our neighbors today. It does not fear any touchstone, does not fear any fire, does not burst asunder by any knocking of the hammer, but it has abided invincible in time past and yet does abide, with the great glory of those that are made rich thereby. White apparel is opposed to the former honors and nakedness, that is, contempt. These garments also Christ will have to be bought from Him, being most precious and most praiseworthy. For what contempt can come to those whom their worthiness has chosen, their learning ordained, their holiness put in authority? Whom many have earnestly desired for their tried godliness do admire for their diligence in teaching, do fear because of the most free truth, and revere as examples of all virtue and honesty. “Be an example,” says Paul, “to the faithful in speech, in conversation, in love, in spirit, in faith, in chastity; let no man despise thy youth,” 1 Timothy 4:12. Behold the way to deliver from contempt. These garments are full of majesty, with which youth being covered is not despised. And so once the prophets went adorned whose hairy garment had more estimation with all men than the silk and vain painting of others. Those wicked men and scorners of the prophets who were together with Jehu, when the prophet, having entered in, did lead him out from the company unwittingly, did show what good opinion of the prophet they had fixed in their minds. “What,” say they, “would that made man have with thee?” Yea rather, why do you make men ask what that made man would have? But their tongue spoke according to their wicked custom: their desire to know did show abundantly what authority and credit they gave to him secretly; whereupon when the message was known assuredly they created him king whom the made man had anointed for king. The Baptist with his leather girdle and garment of camel’s hair was safe from the injury of the priests because of the honor with which the common people honored him. The strength of the divine institution is great in which God himself gives authority either by the voluntary obedience of men or by some punishment inflicted from God. There is no need of the show of earthly riches and honors which at first are wont to dazzle the eyes of the unskillful, but at length when the vanity of it is perceived it is no less despised than frogs fallen from the air. Therefore garments are to be bought from Christ by which alone our nakedness is covered, appearing otherwise very deformed whatever clothes thou put on it. Eye salve of old was all kind of medicine, made in that manner that it might be kept while need should require. At length the name remained chiefly in those which are prepared for the diseases of the eyes because the physicians have used an abundance of it. Here it is applied against blindness, namely the wisdom of the flesh and ignorance of spiritual things. We read that a certain sensible thing was made of the spittle of Christ and of earth, John 9:6, as it were by the knowledge of Christ by the word that proceeds out of his mouth and also the knowledge of ourselves, who in the beginning of the earth savored nothing but the earth. Both these are to be joined together and to be kneaded into one lump; they profit nothing asunder.

For our misery being known particularly brings forth desperation; and Christ being received without the feeling of our own unworthiness is unprofitable and unfruitful. And yet we are not a table to mix and compound these things together, but it must be obtained from him who came into the world to judgment, that those who do not see should see, and those who see should be made blind, John 9:39. First, therefore, we must remove our own wisdom, which as long as it reigns and does possess us so wholly that it leaves no place for true and heavenly. For, O Angel, would you have devised a reformation taken wholly out of your own mind unless you had been full of the opinion of your own wisdom? Overlook your decrees: where is the Spirit called to counsel? By what authority of God’s word is the amending of things confirmed? After what example of the pure church are our matters corrected and amended? There is a deep silence about all these things; nowhere are heard Paul or any other witnesses of the holy truth upon whose credit the things established might rest and stay themselves. I believe you shall scarce find a synod even in the most corrupt times in which divine authority is more dumb and speechless. This opinion is to be laid away, O Angel; you must acknowledge that you are earth, and that you have no eye salve in you until you are mollified with heavenly spit and subdued into a liniment. Depend therefore on the mouth of Christ from which flows that which is profitable to doctrine, to confutation, to correction, to instruction which is in righteousness, so that a man of God may be perfect in every good work, 2 Timothy 3:16–17. From hence is compounded that eye salve which will take away the scales of the eyes and endow you with that sharpness of sight that you may see plainly how you ought to behave yourself in the house of God. Neither must you give ear to them who not only unskillfully but also ungodly cry out that the rules of these things are not to be fetched from this shop. Christ would not set himself forth to be a seller of eye salve unless he had it abundantly enough to help our need, and it were not lawful to buy it from any other. So then the medicine is threefold: gold against poverty, which earthly riches do not ease; white raiment against nakedness, which the honors of the world do not hide; eye salve against blindness, which the wisdom of the flesh does not take away. From which now at length it may be understood that those riches of which, in the former verse, the Angel boasted are not the righteousness of faith alone, as the counterfeit Ambrose speaks unwisely. For those riches rested not on Christ alone. Whereupon he warns that he would buy gold from him, which he should do in vain if before the Angel did abound in the same. But the righteousness of faith has all its treasures placed in Christ alone, of which he is made partaker whoever believes truly and renounces all other righteousness, John 6:48; Romans 3:7. Therefore, O Ribera, draw water from a pumice stone rather than overthrow the righteousness of faith from this place. But such trifles of yours fall upon themselves so that I need not spend time confuting them.

19 As many as I love, &c. An exhortation to use the remedy: and first from the chastising of those whom he loves. A reason indeed of very great moment. Whoever is either among sons or among the reprobates: if he receives no son whom he rebukes and does not chastise, what shall be done with the multitude of the rest? A horrible destruction remains for those whom he will never spare so little, who do not suffer his own children to escape uncorrected. Therefore a chastisement is at hand unless you repent before time, and that very grievous and full of trouble, as the very words themselves do show: which are wont to be used for comfort in a bitter affliction where the mind is so stricken as if it were forsaken by God. Therefore he says they are sons whom he beats with cruel punishments, lest through the grievousness of the punishment they should despair of his fatherly goodness. Therefore it is not time now to strive and to contend with mutual hatred and reproaches, but the ears are to be lifted up to the alarm of Christ, and we must either think forthwith of the remedy or some great and lamentable calamity is to be expected shortly. And it is to be observed that he does rebuke and chasten; that is, convince and punish. These two things are to be joined together. Punishment is unprofitable where words are silent; stripes are fierce. From whence chastisement is well called discipline, wherein the offender feels pain and learns together. But what shall then be the fruit of so long and spiteful contention when the convinced and chastised son shall be compelled, whether he, or not, to sing a contrary song? Were it not better to give now ear to learn than to expect that sorrowful change of our judgment? Although Christ has indeed convinced already, seeing now by the space of many years that many notable men do labour in this thing so that the brethren may understand the truth. What remains now but that at length he fetches out his rods and chastises those whom he has rebuked for so long a time without fruit?

¶ Be hot, therefore; strain therefore your zeal to the utmost. The translation persists in the former metaphor, but the Spirit speaks now properly, teaching that the former heat was nothing else than zeal. Forsake, saith he, your lukewarmness; purge out all the Roman leaven that you may not hang no longer in the midst between the reformed and the anti-Christian church: cast away for his sake honours and riches who for your sake were most despised and most poor. Let faithful pastors be appointed for the several congregations; let them that have charge and rule be compelled unto diligence; let the changers and corrupters of the doctrine be repressed; let the censures be restored to the pastors over their flock. And dispute not with Christ how profitably the polity used of the enemy may be joined with the Gospel. He that reproves in his people the manners of the East and would not have his to be shorn after the similitude of the Gentiles will not easily suffer this society with Antichrist which our carnal wisdom minds. This is the force of this zeal which unless we shall receive forthwith we shall undergo some sharp chastisement.

¶ And repent: repent of the injuries which you have done to the brethren in casting some into prison, in turning others out of their goods, in depriving many of the power to preach the word, in reproaching and traducing all with the odious name of Anabaptists. You know that they have no fellowship with them in any of their errors. Those who reproach your superstitions teach most purely and holy concerning the magistrate: whom they honour no less faithfully and reverently than any other whatsoever. If I should say that he were esteemed more holy and religiously by them than by all others, I would not lie. For those who cleave to God with the firmest minds are such as observe his decrees most closely and in all true obedience yield themselves to him whom they acknowledge to be ordained of God among men in his fear. That was a notable calumny whereby both you have deceived the prince and also procured hatred to your brethren. But you saw that this weapon was most ready at hand and to them hurtful above all others. Repent and wash away your former offences with tears; forget your riches, the more you love, the more pain you shall feel. It is forsaken with much ado where it cleaves so near the heart. But Christ is determined, unless you repent in time, to spew you out of his mouth.

20 Behold I stand at the door: a second reason persuading to use the remedy taken from the readiness of Christ to dwell with them who shall receive him which belongs to every one of the members. That former respected properly the angel; but why does he say that he stands at the door and knocks? Why does he not open the door and go straight in, especially seeing he has the key of David with which he opens and no man shuts? These things are spoken most elegantly and most significantly in respect of the Laodicean church and ours in which Christ stands at the doors, an entry in some sort stopped up against him. The Philadelphia church in which once flourished God’s ordinance and in whose antitype it is forced at this day all the relics of Antichrist being thrust forth has the door unlocked and opened; and especially because of the true use of excommunication restored whereby the gates of heaven are both shut and opened, and also the doors of every one’s conscience are opened so that Christ may pass in without any tarrying. For where good heed is taken to every one’s manners and according to the present occasion men are admonished, reproved, cut off, received again, and the other things are performed faithfully and diligently with the regard had of every one’s salvation, all doors and bars of the heart are cast down and removed, and in very truth the gates then lift up their heads that the King of Glory may enter in. But when England is lukewarm because of the contagion of the Roman government (as once Laodicea for some such like mixture) and has no administration of the censures granted unto lawful pastors as Christ has appointed: as often as the word is preached Christ stands knocking as it were at the doors shut, to whom no other way is open into men’s hearts than by the word; whose power we read to have been great once when in one sermon three thousand were converted, Acts 2:41. Neither is it at this day of itself less mighty: yet there is a diverse reason of a church to be gathered and one gathered. God shows himself extraordinarily bountiful in inviting his people which after he has gathered together he will have them to grow by the way appointed. As touching the fruit of the gospel therefore the people receive no less loss of so excellent an ordinance than the angel acknowledges himself maimed and lame being spoiled of his lawful power. This key is wanting to our church and therefore it is no marvel if Christ be hindered that he cannot enter in readily seeing the doors are shut. But are we then destitute of every good thing? In no wise; for we enjoy still a double good thing wholesome to the elect: the first of which is the going in of Christ unto those that do open to him. The second is their most sweet setting down with Christ. That is the most sweet solace of receiving Christ which the saints perceive as often as at the word preached they feel their hearts to be opened by faith by the work of the Spirit. For then he enters in and suppers with us, imparting himself most benignly and sweetly, even as he bade Zacchaeus desiring to see him and climbing up on a wild fig tree to come down and to make ready for him entertainment at his house, Luke 19:5. And he suppers not going away scot‑free who does give them that thus embrace him that they be made the sons of God, John 1:12. He again entertains us that we may sup together with him as often as with pure minds we come to the sacrament of the supper wherein he feeds us with his own flesh and blood most sumptuous delicious dainties above all that can be spoken or thought.

In which sense it is spoken in Luke 13:29, “Then they shall come from the east and from the west and from the north and from the south and shall sit down in the kingdom of God,” that is, men shall assemble together to the gospel from all quarters, shall embrace the doctrine of the kingdom and shall be partakers of Christ truly whose pledges they shall take, bread and wine, sitting down at his table in celebrating his sacred supper. For he speaks of the calling of the Gentiles whose faith and assenting to the whole truth he signifies by one sacramental action. These guests now Christ would call when in the meantime the Jews of whom he speaks in the parable did abhor and despise the way of salvation as we see it has come to pass now for the space of many ages. Whereunto pertains that which in the same place the Jews excluded do allege requiring an entry for themselves because of their former familiarity in eating and drinking in his sight, verse 26, as though they should say, “O Lord, we communicating at your table have feasted merrily with you in eating of your sacrifices; wilt thou lock the door now against us?” For in this respect the meat of the sacrifices was the same thing to the Jews that the bread and wine is to us. Neither are these things notwithstanding so to be taken as though the elect were limited within the bounds of this life; but because the supper which is made on earth is a pledge of the eternal feast in the heavens. These things therefore prove that a double and great good thing abides in the English church, that is to say the preaching of the word and the lawful administration of the sacraments. In both which Christ bestows himself upon his people, keeping a mutual feast with them; he first being received by us by hearing, secondly entertaining us again with the supper of his body. O we therefore most impure as often as we fly from and forsake hearing of the word, for we refuse Christ to be our guest: O wicked despisers that we are as often as we withdraw ourselves from receiving the sacrament with our brethren, for we despise Christ bidding us to supper. But these things are added for the singular comfort of the godly. For who would not quake and think of flying very quickly from this church when they should hear that the condition of the ministers is hated by Christ who, if not repenting, will vomit out of his mouth shortly unless by the words of Christ himself they were assured of their communicating with him? Praise be to you therefore, most meek Lamb, who finding the door shut does not depart quickly being moved with anger and fury and deprive us of all means of salvation but leaves yet an abundance of yourself to all that do open to you knocking by the word and despise not your sweetest invitation by the sacraments.

Therefore wicked and blasphemous is their error who fall away so from this church as if Christ were banished wholly from here and that there could be no hope of salvation for them that tarry there. Let them mind here Christ feasting with his people. Will they be ashamed to sit down there where they see Christ not ashamed? Are they holier and purer than he? But why do they not convince themselves by their own experience? They cannot deny but that they believed in Christ before they made a separation from us: where did this faith come from? Came it not from our preaching in our church? Can any then preach except he be sent? Romans 10:13 etc. Why then do they so perversely refuse for some blemish in the outward calling that word whose divine force they feel in their hearts? Although the fruit itself do no more free from blame our corruptions than a true child adultery. And therefore neither may we either take pleasure in them nor they forsake and fall away from us for some blemishes. Wherefore return to the unity of the church which hath begotten and nourished you. If you fly from this Christ who suppers with his elect in our assemblies and welcomes them again, you shall find him nowhere. In the meantime let us also mind how great evil we call for upon ourselves who by holding hard our superstitions do throw our brethren into so great danger. Certainly if that has any weight which the truth himself once confirmed, it would be better for such men that a millstone being hanged about their necks they were drowned in the bottom of the sea, Matthew 18:6. I wish health of mind to both. But moreover this place is to be delivered from the fraud of the Papists who will have it to be in the power of men to open to Christ knocking. “Whether,” says Bellarmine, “does he not know that they cannot open? Should he not be a fool who would knock at the door of his neighbour if he knew certainly that none were within who could open?” in his first book of Grace and Free Will, chap. 11. I answer: he should not without cause be a fool if his only end of knocking were that he might enter in; but Christ knocks at the door of the reprobates whom he knows neither to be willing nor able to open not that he may enter in but partly that he may upbraid them with their impotency gotten by their own fault, partly that he may increase their condemnation. For so speaks the evangelist expressly, “Therefore they could not believe,” John 12:34. Why then uses he words to them who have not ability to believe? Christ himself shows: “If I had not come,” says he, “and spoken unto them, they should not have had sin; but now they have no cloak for their sin,” John 15:22. Therefore he spoke unto them that for the contempt and hatred of his only begotten son their condemnation might be the greater. Such are the powers of the natural man as is the love of the truth in the Papists who seeing it refuse it wickedly.

21 To him who overcomes I will give a seat: word for word in the Greek is “He who overcomes I will give him,” by the nominative case absolute, as was observed before, Chapter 2:26. This third reason is taken from the reward of being a companion and partaker of his throne: not because the glory of every one of the children shall be equal to the honor of the man Christ, but because the glory and majesty of the head shall redound to every one of the members. Therefore the thrones are not peculiar to the twelve apostles of which see Matthew 19:28 but common to all the elect. Although in a certain peculiar manner they are attributed in the same place to the apostles, as it may be we will show in another place. And we have said often that the rewards are fitted unto the times and to contain a prophecy which is here also to be respected. Christ therefore mentions the throne which he obtained after his sacrifice finished on the cross showing that the like things are to be endured also of his; afterward they shall be partakers of his throne. Therefore by this making mention of it he lessens the affliction and so the consolation of it he sets himself for an example as though he should bid us look upon him and not to be overcome by any troubles when we see that he ascended into his throne of supreme dignity by this way. And we know how much this contending for reformation has cost many and excellent men whose sufferings shall not be forgotten although they be not recited of me. Only let them comfort their faintness of heart with the expectation of his throne. What though they be trodden under foot while they shall see others to flourish with the dignity of peers of the realm? Christ has prepared for them a throne with himself. Let no man regard an earthly chair: as hitherto they have confirmed abundantly that they are far off from such desire, whatsoever ambitious men prate otherwise who do conjecture of others by themselves.

22 Let him who has an ear hear: now therefore whoever has felt Christ to be your guest and has tasted again the dainties of his table, lift up your ears and attend to what the Spirit says to the churches. Let man go and rest not in him but regard the convenience of all things from the beginning to the end. And complain not of newness and strangeness as though you would appoint Christ to whom and when he should reveal his secrets. We know that some things have been sealed up until the appointed time. But if it is necessary that you confess it to be a divine truth, let us all endeavor earnestly, princes, peers, angels, people, so that we may turn away the evil that hangs over our heads. What a horrible thing it is to be vomited out of Christ’s mouth with loathing and abhorrence? The land once cast out the Canaanites and they were destroyed utterly. Shall their punishment be lighter for those whom Christ himself will spew out instead of the land? Therefore let us use the remedy seriously. We need zeal to attain a full reformation: we hang yet between heaven and hell: the contagious vapor of the Roman marshes molests and annoys us; our silver until now is foul with dross; our wine is mixed with water; Christ will no longer tolerate such angels that are in the middle. What if this admonition is the last token and sign to you of being wary? Let us therefore listen and not sharpen our teeth against the stone that is hurled: but let us quake in fear of the hand that threw it. You, O Christ, who once took Lot by the hand to pull him out of the city, open our hearts that are slow and extend the time that we may obey your warnings and exhortations.

在云服务器端口25受限环境下部署Mailcow邮件服务器

背景与挑战

在现代云计算环境中，主流云服务提供商（如GCP、AWS）为了防止垃圾邮件传播，普遍禁用了虚拟机实例的端口25出站流量。这给自建邮件服务器带来了巨大挑战。本文记录了在这种受限环境下，通过日本ConoHa.jp服务器作为SMTP中继，成功部署Mailcow邮件服务器的完整过程。

系统架构设计

graph TB
    subgraph "外部网络"
        Client[用户客户端
IMAP/SMTP]
        ExtMail[外部邮件服务
Gmail/Outlook]
        Internet[互联网]
    end
    
    subgraph "ConoHa 中继服务器 (10.8.0.34)"
        ConoHA[Ubuntu Server
Postfix + iptables]
        VPN1[OpenVPN Client]
    end
    
    subgraph "Mailcow 服务器 (10.8.0.33)"
        Mailcow[Mailcow Docker
Postfix + Dovecot]
        VPN2[OpenVPN Client]
    end
    
    subgraph "VPN 隧道网络 (10.8.0.0/24)"
        VPNTunnel[加密隧道]
    end
    
    %% 连接关系
    Client -->|IMAP/SMTP 连接| ConoHA
    ConoHA <-->|VPN 隧道| VPNTunnel
    VPNTunnel <-->|VPN 隧道| VPN2
    VPN1 -.-> VPNTunnel
    VPN2 -.-> Mailcow
    ConoHA -->|端口转发| Internet
    Internet <-->|SMTP| ExtMail
    
    %% 数据流标注
    Client -.->|1\. 用户连接
端口: 993,143,587,465| ConoHA
    ConoHA -.->|2\. 入站邮件转发
端口: 25| Mailcow
    Mailcow -.->|3\. 出站邮件中继
relayhost: 10.8.0.34:25| ConoHA
    ConoHA -.->|4\. 外网发送
端口: 25| ExtMail
    
    style Client fill:#e1f5fe
    style ExtMail fill:#e8f5e8
    style ConoHA fill:#fff3e0
    style Mailcow fill:#f3e5f5
    style VPNTunnel fill:#e0f2f1

数据流向说明：

1. 入站邮件: 外网 → ConoHa(iptables DNAT) → VPN → Mailcow
2. 出站邮件: Mailcow → VPN → ConoHa(Postfix relay) → 外网
3. 用户连接: 客户端 → ConoHa(端口转发) → VPN → Mailcow

核心组件

• 主服务器 (10.8.0.33): Mailcow Docker化邮件服务器，运行在macOS
• 中继服务器 (10.8.0.34): ConoHa.jp Ubuntu服务器，负责端口25流量转发
• VPN网络: OpenVPN连接两台服务器，提供安全的内网通信

部署步骤

1. ConoHa中继服务器配置

1.1 安装OpenVPN 3客户端

1
2
3
4
5
6
7

# 添加OpenVPN官方源
sudo mkdir -p /etc/apt/keyrings && curl -fsSL https://packages.openvpn.net/packages-repo.gpg | sudo tee /etc/apt/keyrings/openvpn.asc

DISTRO=$(lsb_release -c | awk '{print $2}')
echo "deb [signed-by=/etc/apt/keyrings/openvpn.asc] https://packages.openvpn.net/openvpn3/debian $DISTRO main" | sudo tee /etc/apt/sources.list.d/openvpn-packages.list

sudo apt update && sudo apt install openvpn3

1.2 配置VPN连接

1
2
3
4
5
6

# 导入VPN配置文件
openvpn3 config-import --config free-smtp-server.ovpn --name dtype --persistent
openvpn3 config-acl --show --lock-down true --grant root --config dtype

# 设置开机自启
sudo systemctl enable --now openvpn3-session@dtype.service

1.3 配置网络转发

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 启用IP转发
echo 'net.ipv4.ip_forward=1' | sudo tee -a /etc/sysctl.conf
sudo sysctl -p

# 配置入站邮件服务端口转发
sudo iptables -t nat -A PREROUTING -p tcp --dport 993 -j DNAT --to-destination 10.8.0.33:993  # IMAPS
sudo iptables -t nat -A PREROUTING -p tcp --dport 143 -j DNAT --to-destination 10.8.0.33:143  # IMAP
sudo iptables -t nat -A PREROUTING -p tcp --dport 587 -j DNAT --to-destination 10.8.0.33:587  # SMTP STARTTLS
sudo iptables -t nat -A PREROUTING -p tcp --dport 465 -j DNAT --to-destination 10.8.0.33:465  # SMTPS

# 配置入站邮件接收转发（排除内网流量避免循环）
sudo iptables -t nat -A PREROUTING ! -s 10.8.0.0/24 -p tcp --dport 25 -j DNAT --to-destination 10.8.0.33:25

# 配置转发规则
sudo iptables -A FORWARD -p tcp -d 10.8.0.33 -m multiport --dports 993,143,587,465,25 -j ACCEPT

# 配置出站NAT
sudo iptables -t nat -A POSTROUTING -o tun0 -j MASQUERADE

1.4 安装和配置Postfix中继服务

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 安装Postfix
sudo apt update && sudo apt install postfix

# 配置为邮件中继服务器
sudo postconf -e "mynetworks = 127.0.0.0/8 10.8.0.33/32"
sudo postconf -e "inet_interfaces = all"
sudo postconf -e "relayhost = "
sudo postconf -e "mydestination = localhost"

# 重启服务
sudo systemctl restart postfix

# 配置防火墙
sudo ufw allow from 10.8.0.33 to any port 25

2. Mailcow服务器配置

2.1 OpenVPN客户端配置

在.ovpn配置文件中添加：

1
2

route 10.8.0.0 255.255.255.0
route-nopull

2.2 出站邮件中继配置

方案一：使用内网Postfix中继（推荐）

1
2
3

# 配置Mailcow使用ConoHa服务器作为中继
docker-compose exec postfix-mailcow postconf -e "relayhost = [10.8.0.34]:25"
docker-compose restart postfix-mailcow

方案二：使用Gmail SMTP中继（备选）

1
2
3
4
5
6
7
8
9
10
11
12
13

# 配置Gmail作为SMTP中继
docker-compose exec postfix-mailcow postconf -e 'relayhost = [smtp.gmail.com]:587'        
docker-compose exec postfix-mailcow postconf -e 'smtp_use_tls = yes'
docker-compose exec postfix-mailcow postconf -e 'smtp_sasl_auth_enable = yes'
docker-compose exec postfix-mailcow postconf -e 'smtp_sasl_password_maps = hash:/etc/postfix/sasl_passwd'
docker-compose exec postfix-mailcow postconf -e 'smtp_tls_security_level = encrypt'

# 创建Gmail认证文件
echo "[smtp.gmail.com]:587 your-email@gmail.com:your-app-password" | docker-compose exec -T postfix-mailcow tee /etc/postfix/sasl_passwd
docker-compose exec postfix-mailcow postmap /etc/postfix/sasl_passwd
docker-compose exec postfix-mailcow chmod 600 /etc/postfix/sasl_passwd
docker-compose exec postfix-mailcow chmod 600 /etc/postfix/sasl_passwd.db
docker-compose restart postfix-mailcow

2.3 Linux环境下的iptables方案（可选）

如果Mailcow部署在Linux系统上，可以使用iptables在宿主机级别进行流量重定向：

10.8.0.33 (Mailcow服务器) 的设置：

1
2
3
4
5

# 将出站端口25流量重定向到中继服务器
sudo iptables -t nat -A OUTPUT -p tcp --dport 25 -j DNAT --to-destination 10.8.0.34:25

# 对重定向的流量进行源地址转换
sudo iptables -t nat -A POSTROUTING -d 10.8.0.34 -p tcp --dport 25 -j MASQUERADE

10.8.0.34 (中继服务器) 的设置：

1
2
3
4
5

# 允许来自Mailcow服务器的转发流量
sudo iptables -A FORWARD -s 10.8.0.33 -p tcp --dport 25 -j ACCEPT

# 对来自Mailcow的流量进行源地址转换后转发到外网
sudo iptables -t nat -A POSTROUTING -s 10.8.0.33 -p tcp --dport 25 -j MASQUERADE

这种方案的优势是在网络层直接处理，无需修改应用配置，但需要Linux系统支持。

故障排除经验

问题1：防火墙阻止连接

现象: Connection refused错误

1

(connect to 10.8.0.34[10.8.0.34]:25: Connection refused)

解决方案:

1
2
3
4
5

# 检查服务监听状态
sudo ss -tlnp | grep :25

# 配置UFW防火墙
sudo ufw allow from 10.8.0.33 to any port 25

问题2：避免路由循环

现象: 邮件在两个服务器间循环
解决方案: 在iptables PREROUTING规则中排除内网源地址

1

sudo iptables -t nat -A PREROUTING ! -s 10.8.0.0/24 -p tcp --dport 25 -j DNAT --to-destination 10.8.0.33:25

最终配置验证

测试入站邮件

1
2
3

# 从外部发送邮件到 your-email@your-domain.com
# 检查Mailcow日志
docker-compose logs -f postfix-mailcow

测试出站邮件

1
2
3
4
5

# 检查邮件队列
docker-compose exec postfix-mailcow postqueue -p

# 强制发送队列中的邮件
docker-compose exec postfix-mailcow postqueue -f

验证中继工作状态

1
2
3
4

# 查看成功的中继日志
docker-compose logs postfix-mailcow | grep "relay=10.8.0.34"
# 应该看到类似输出：
# status=sent (250 2.0.0 Ok: queued as XXXXX)

性能与安全考量

1. 网络延迟: VPN隧道会增加约20-50ms延迟，但对邮件服务影响较小
2. 单点故障: ConoHa服务器是关键节点，建议配置监控和备份方案
3. 安全性: 所有邮件流量通过加密VPN传输，相比直连更安全
4. 成本优化: ConoHa服务器选择最低配置即可满足中继需求

总结

通过VPN+中继服务器的架构，成功解决了云服务商端口25限制的问题。该方案具有以下优势：

• 灵活性: 可以随时更换云服务商而不影响邮件服务
• 可扩展性: 中继服务器可以同时为多个Mailcow实例提供服务
• 成本效益: 相比企业级邮件服务，成本显著降低
• 完全控制: 保持对邮件数据和配置的完全控制权

这套解决方案为在受限云环境中部署自托管邮件服务器提供了可行的技术路径。